1. 📘 Учебник
2. § 6. Треугольники: определение, свойства, задачи на построение

Треугольники

Определение.

Треугольник есть фигура, ограниченная тремя прямыми линиями, называемыми его сторонами.

Определение.

Прямоугольный треугольник есть треугольник, один угол которого прямой.

Определение.

Равноугольный треугольник есть треугольник, у которого все углы равны.

• Теорема.

  Сумма трех углов всякого треугольника равна двум прямым углам.

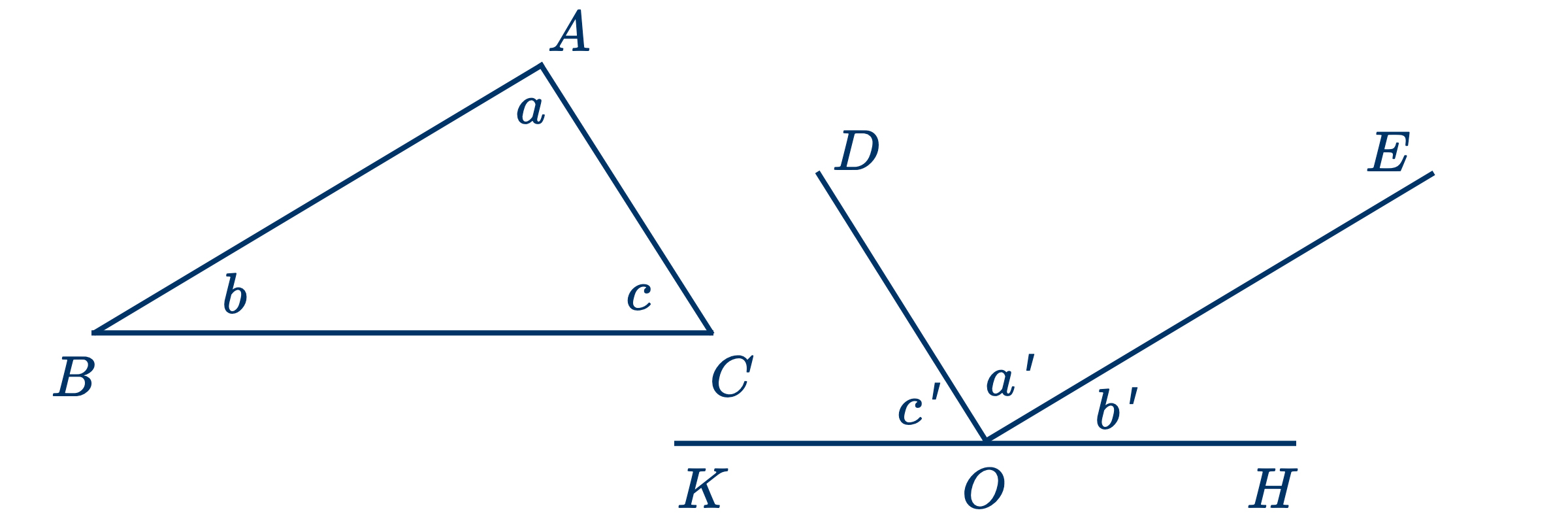
Дано: треугольник $ABC$ и его углы $a, b, c$.
Доказать, что $a+b+c=2$ прямым углам.

Проводим прямую $KH$ параллельно $BC$, и из какой-нибудь точки на этой линии, положим $O$, проводим $OE$ и $OD$ параллельно соответственным сторонам $BA$ и $CA$.
Тогда $⇒\begin{cases} a=a' \\ b=b' \\ c=c' \end{cases}$ (см. теорему .) Так как их стороны параллельны в том же порядке.
Отсюда $a+b+c=a'+b'+c'$. $\bigstar$
Но $a'+b'+c'=2$ прямым углам. (см. следствие теоремы .)
Отсюда $a+b+c=2$ прямым углам. (см. акс. 1.)
Q.E.D.

Следствие.

Если продолжить одну из сторон треугольника, то образовавшийся таким образом внешний угол равен сумме двух несмежных к нему внутренних углов (и, следовательно, больше каждого из них).

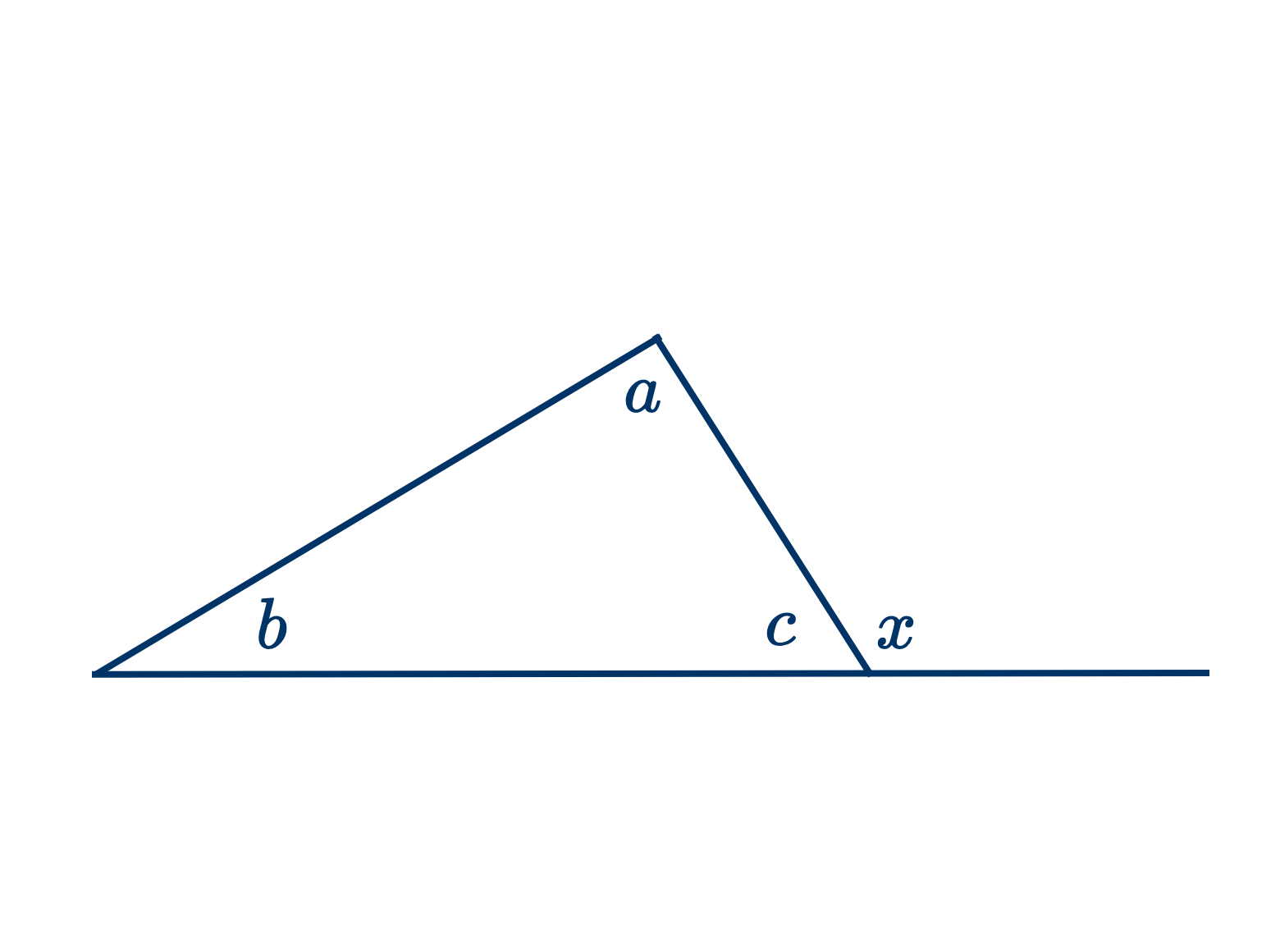
Схема доказательства: $a+b+c=2$ прямым углам $=x+c$, отсюда $a+b=x$. Объясните почему.

Следствие.

Если дана сумма двух углов треугольника, то третий угол можно получить, отняв сумму от двух прямых углов. Какая аксиома применяется?

Следствие.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то и третьи углы равны. Какие две аксиомы применяются?

Следствие.

Треугольник может иметь только один прямой или тупой угол.

Следствие.

В прямоугольном треугольнике сумма двух углов, кроме прямого, равна прямому углу.

Следствие.

В равностороннем тругольнике каждый угол составляет одну треть двух прямых углов, следовательно, равняется двум третям прямого угла.

Определение.

Многоугольник есть плоская фигура, ограниченная прямыми линиями, называемыми ее сторонами. Многоугольник называется выпуклым, если прямая может пересечь его стороны только в двух точках.

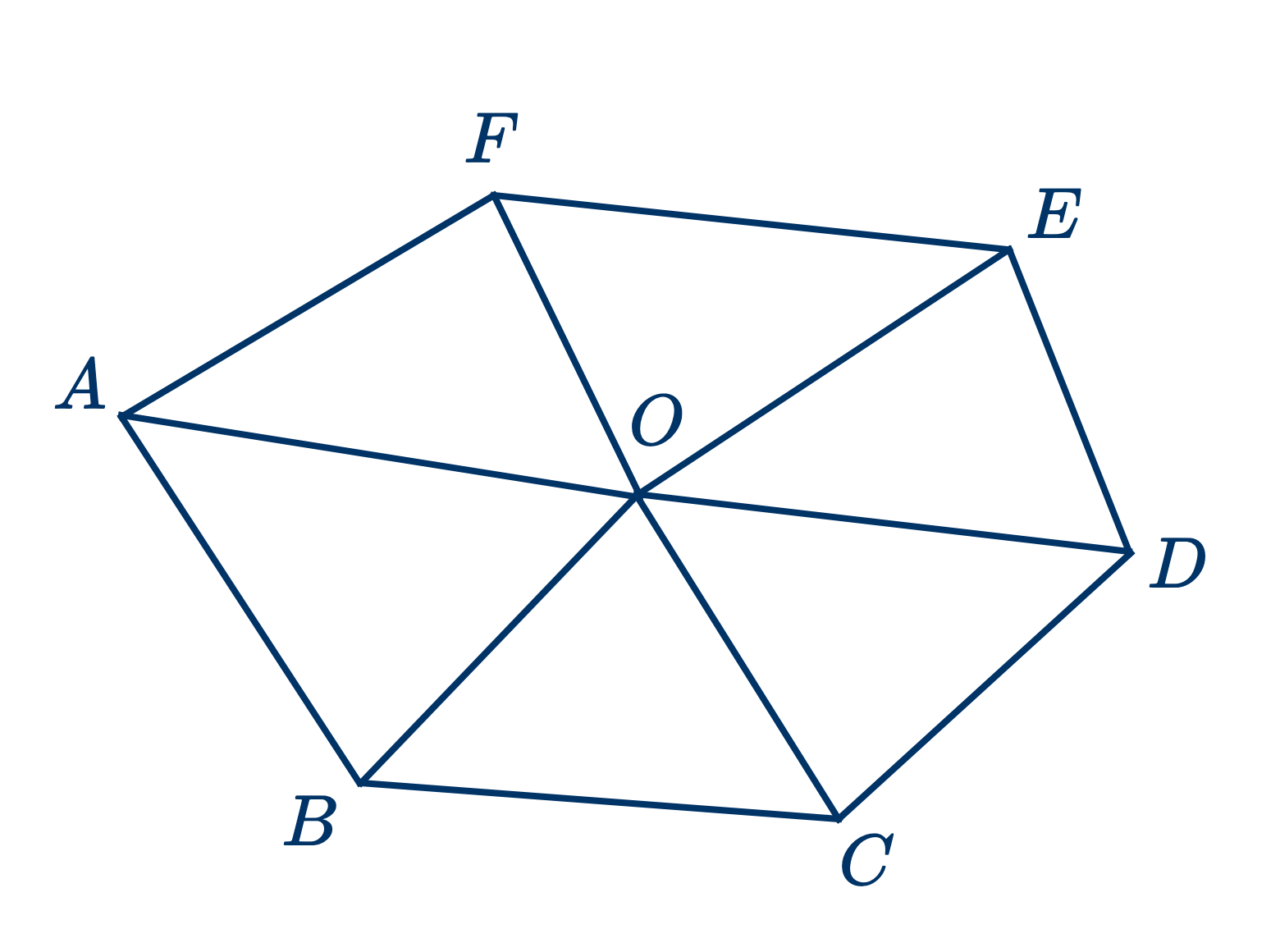
Дано: $ABCDE$ — многоугольник, имеющий $n$ сторон.
Доказать, что сумма его углов $=(2n-4)$ прямым углам.

Из какой-нибудь точки $O$ внутри многоугольника проводим прямые ко всем вершинам, образуя $n$ треугольников.
Сумма углов каждого треугольника равна $2$ прямым углам. (см. теорему .)
Отсюда сумма углов $n$ треугольников равна $2n$ прямым углам.
Но углы многоугольника в то же время углы треугольников, исключая углы вокруг точки $O$, которые равняются $4$ прямым углам. (см. следствие теоремы .)
Отсюда сумма углов многоугольника есть $(2n-4)$ прямых углов.
Q.E.D.

Определение.

Четырехугольником называется многоугольник, имеющий четыре стороны, пятиугольником — пять сторон, шестиугольником — шесть, восьмиугольником — восемь, десятиугольником — десять, двенадцатиугольником — двенадцать, пятнадцатиугольником — пятнадцать сторон.

Вопрос.

Чему равняется сумма углов четырехугольника? пятиугольника? шестиугольника?

• Теорема.

  Если каждую сторону многоугольника продолжить в одном направлении, то сумма образовавшихся при этом внешних углов равна четырем прямым углам..

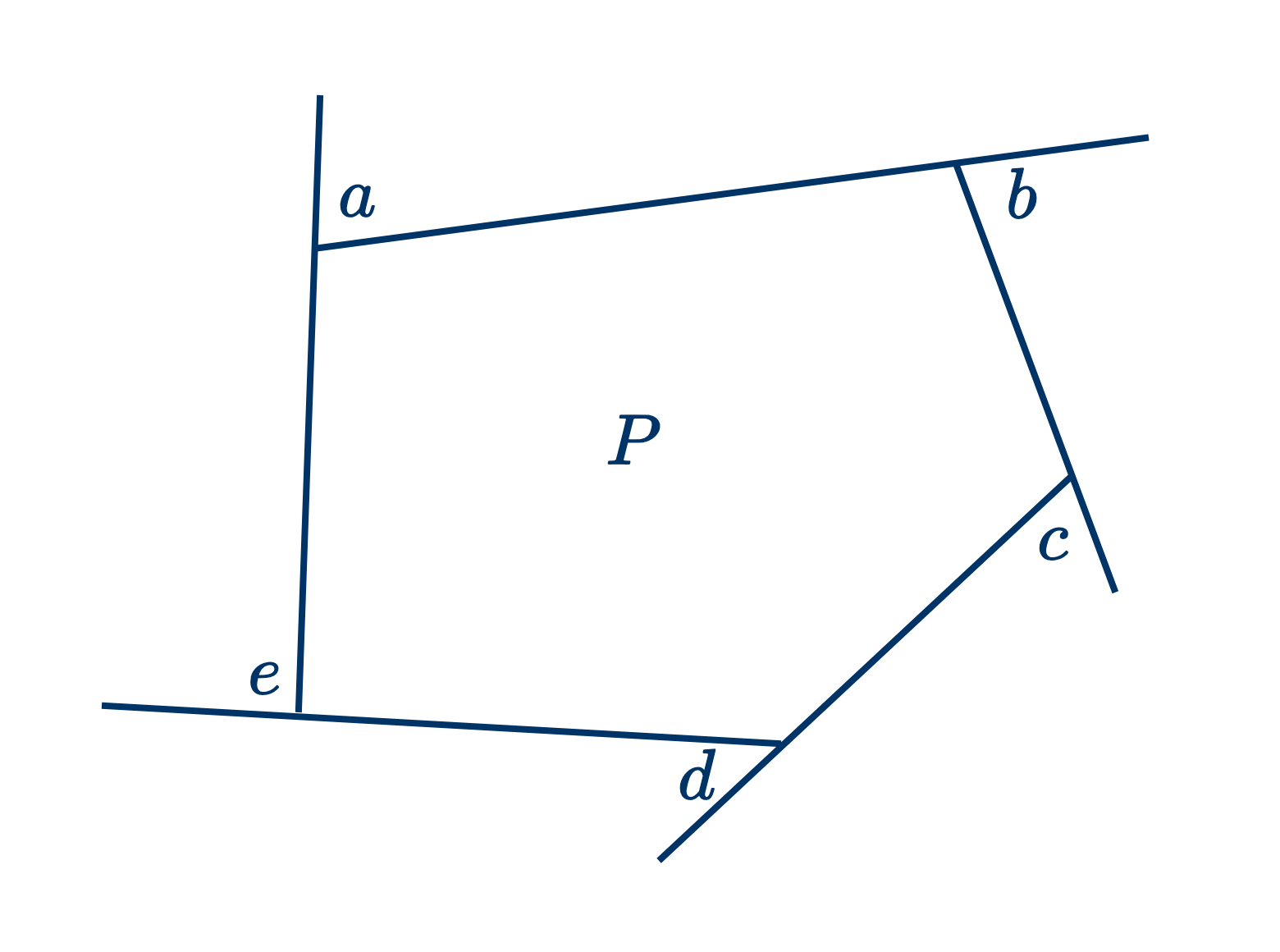
Дано: многоугольник $P$ с последовательными внешними углами $a, b, c, d, e.$
Доказать, что $a+b+c+d+e=4$ прямым углам.

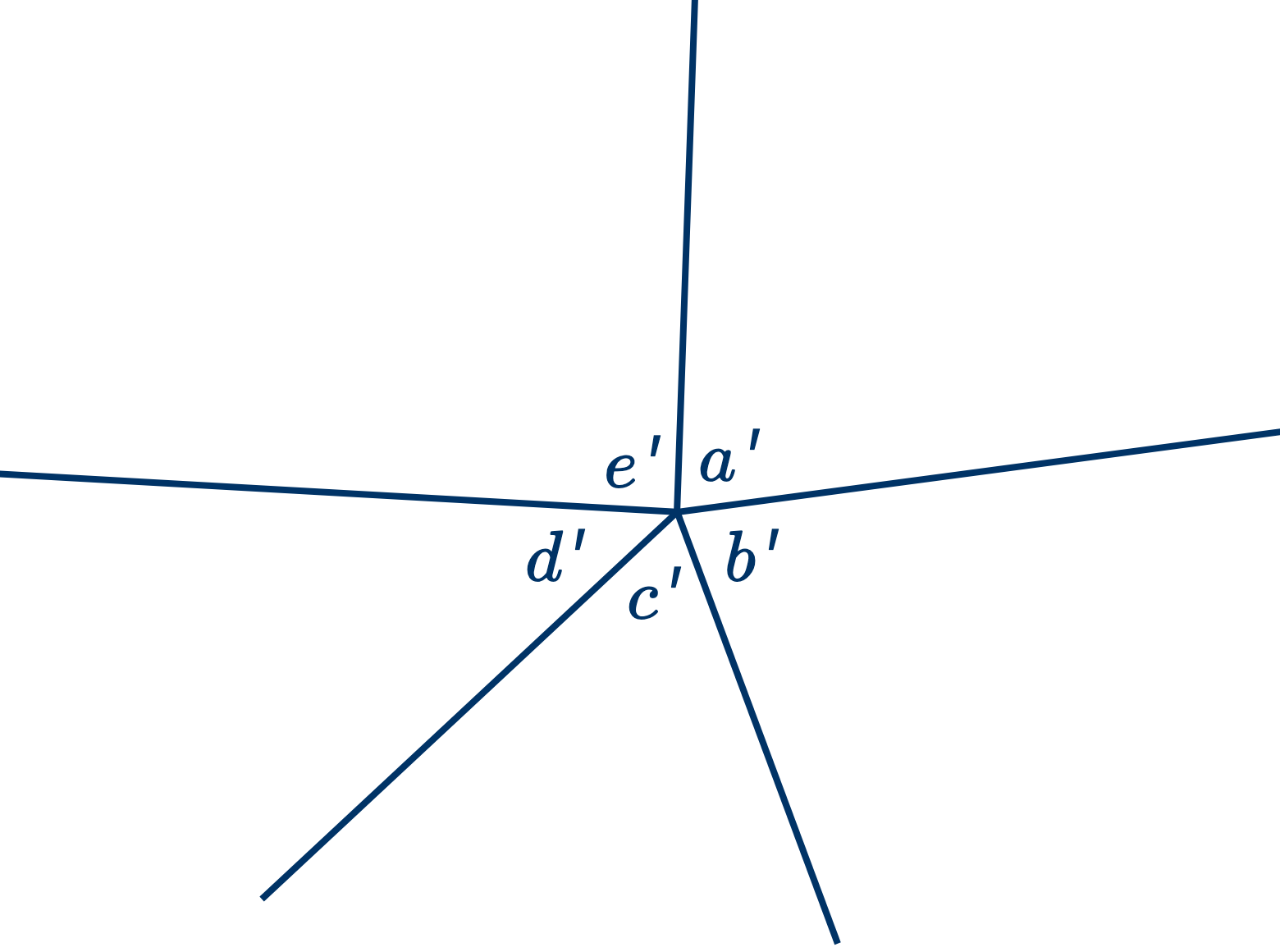
Через какую-нибудь точку $O$ проводим линии параллельные соответственным продолжениям его сторон.
Тогда $⇒\begin{cases} a=a' \\ b=b' \\ c=c' \\ ... \end{cases}$ (см. теорему .)
Отсюда $a+b+c+....=a'+b'+c'+....$ (см. акс. 2.)
Но $a'+b'+c'+....=4$ прямым углам. (см. следствие теоремы .)
Поэтому $a+b+c+....=4$ прямым углам (см. акс. 1.)
Q.E.D.

Определение.

Равнобедренным треугольником называется такой треугольник, у которого две стороны равны. Третья сторона называется основанием. Противоположная вершина называется вершиной равнобедренного треугольника; угол при ней называется углом при вершине. Равносторонним треугольником называется такой треугольник, у которого три стороны равны.

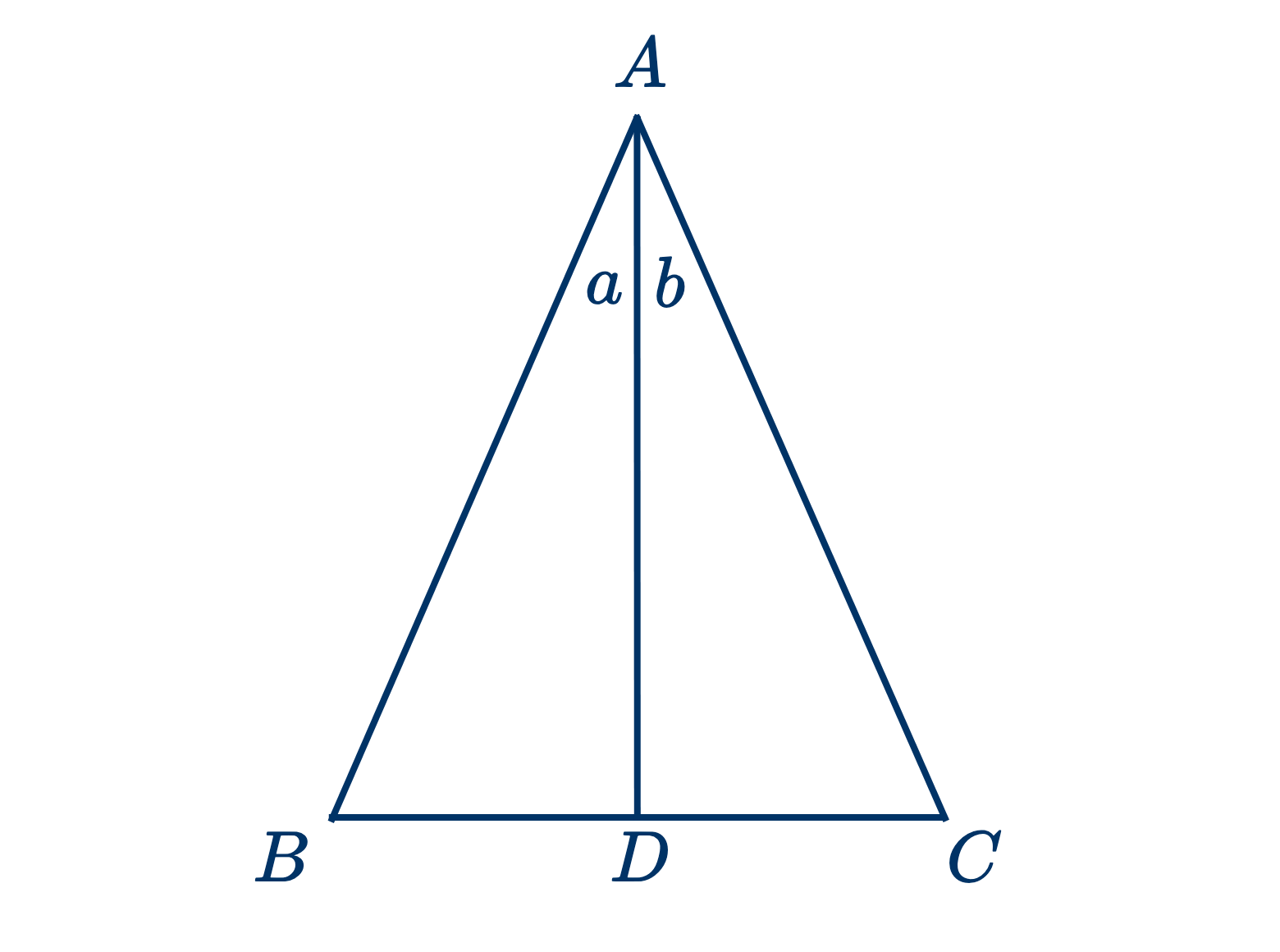
Дано: $ABC$ равнобедренный треугольник, $AB$ и $AC$ его равные стороны.
Доказать, что углы при основании равны, т.е. $\angle B=\angle C$.

Положим, что $AD$ делит $\angle A$ пополам.
Около $AD$, как оси, вращаем фигуру $ADC$, пока она не совпадет с плоскостью $ADB$.
$AC$ пойдет вдоль $AB$. (Так как угол $a=b$, по построению.)
$C$ упадет в $B$. (Так как $AB=AC$ по условиюю.)
$DB$ совпадет с $DC$. (см. акс. прямой.) (Их концы находятся в одних и тех же точках.)
Отсюда $\angle B=\angle C$. (см. опред.)
Q.E.D.

Следствие.

Прямая, делящая угол при вершине равнобедренного треугольника пополам, делит и его основание пополам.

Указание.

Покажите, как это вывести, пользуясь предыдущим доказательством.

Следствие.

Прямая, соединяющая середину основания с вершиной равнобедренного треугольника, есть биссектриса угла при вершине.

Указание.

Проведите прямую, которая должна разделить пополам угол при вершине, и докажите, что она совпадает с данной прямой.

Следствие.

Каждый равносторонний треугольник в то же время равноугольный, а каждый его угол равен трети двух прямых углов.

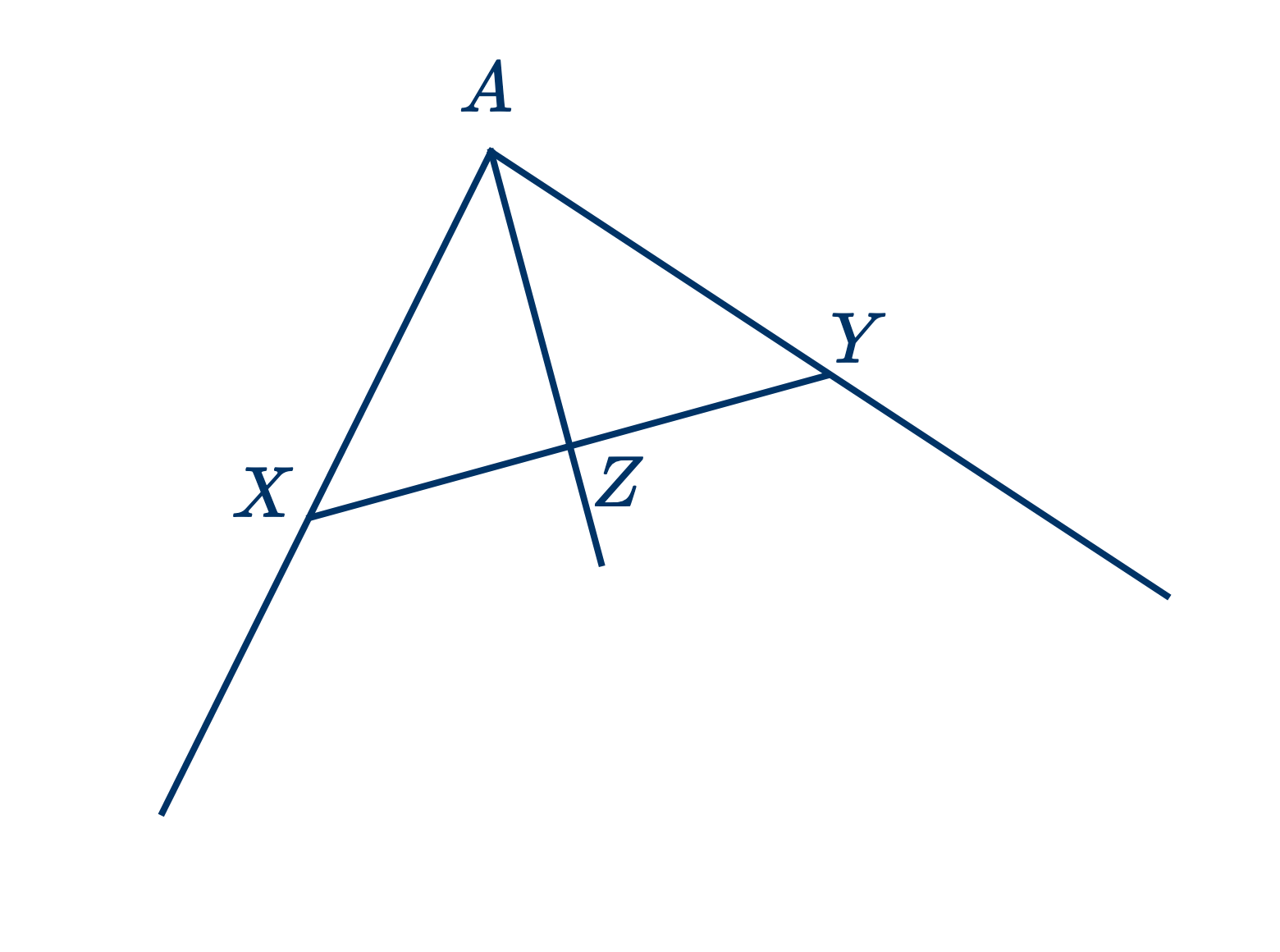
• Теорема.

  Если две стороны треугольника неравны, то противоположные углы также неравны, и против большей стороны лежит больший угол.

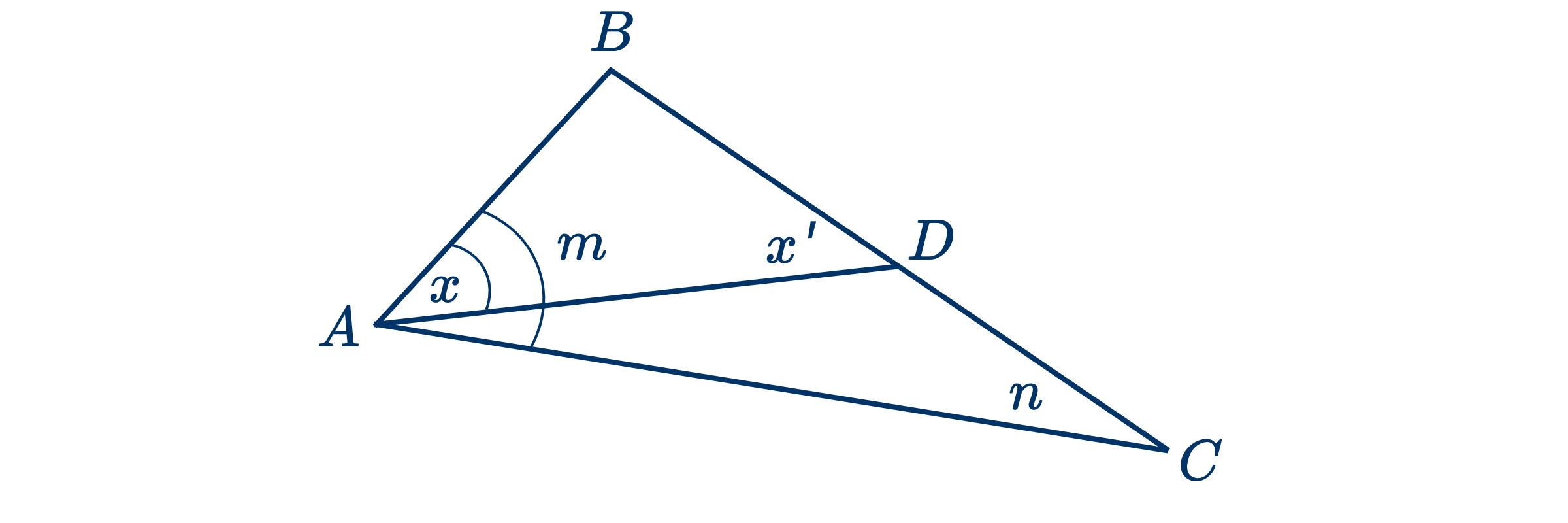
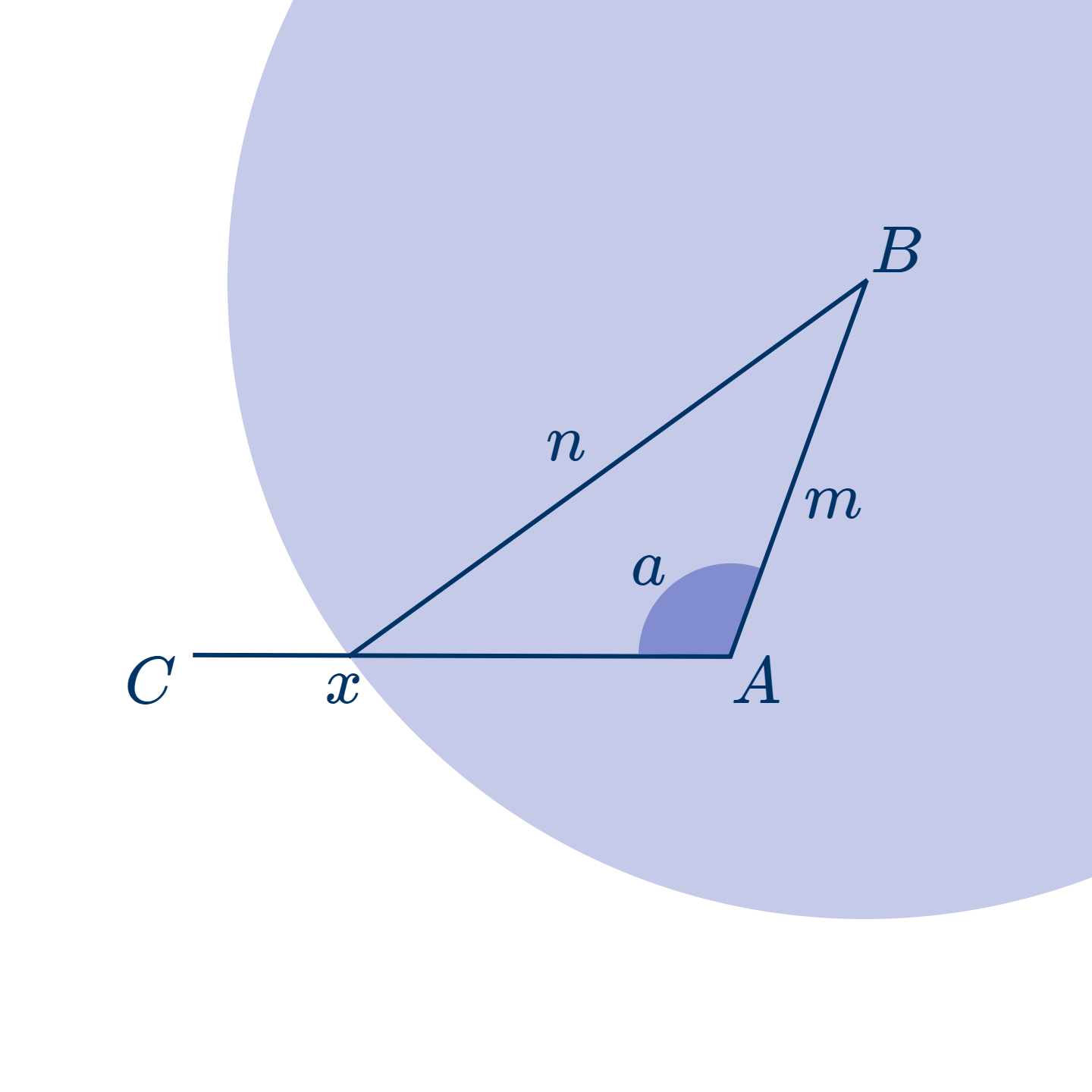
Дано: в треугольнике $ABC$ сторона $BC>BA$.
Доказать, что угол $m>n$.

На $BC$ откладываем $BD=BA$ и проводим $AD$.
Тогда $x=x'$ как углы при основании равнобедренного треугольника (см. теорему .)
Но $x'>n$, внешний угол треугольника $(ADC)$ больше каждого из несмежных к нему внутрненних углов. (см. следствие теоремы .)
Подставляя $x$ вместо $x'$, где $x>n$.
Но $m>x.$ (см. акс. 10.)
Отсюда $m>n$. (см. акс. 13.)
Q.E.D.

Данная теорема является обратною к теореме

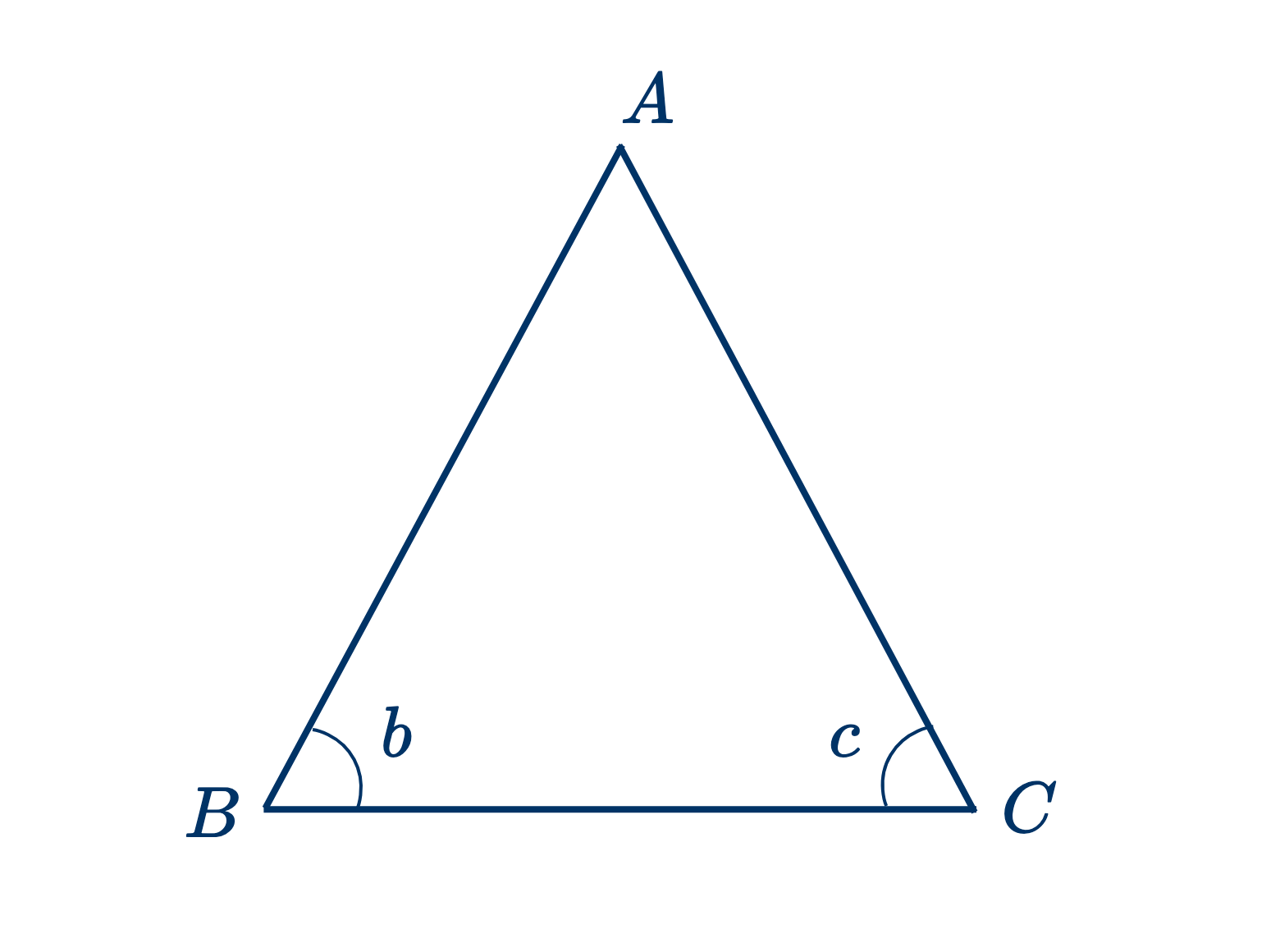
Дано: в треугольнике $ABC$ угол $b=c$.
Доказать, что сторона $AC=AB$.

Если бы $AC$ и $AB$ были неравны, $b$ и $c$ также были бы неравны. (см. теорему .)
Но это противоречит условию, что угол $b=c$.
Отсюда $AC=AB$.
Q.E.D.

Данная теорема является обратною к теореме

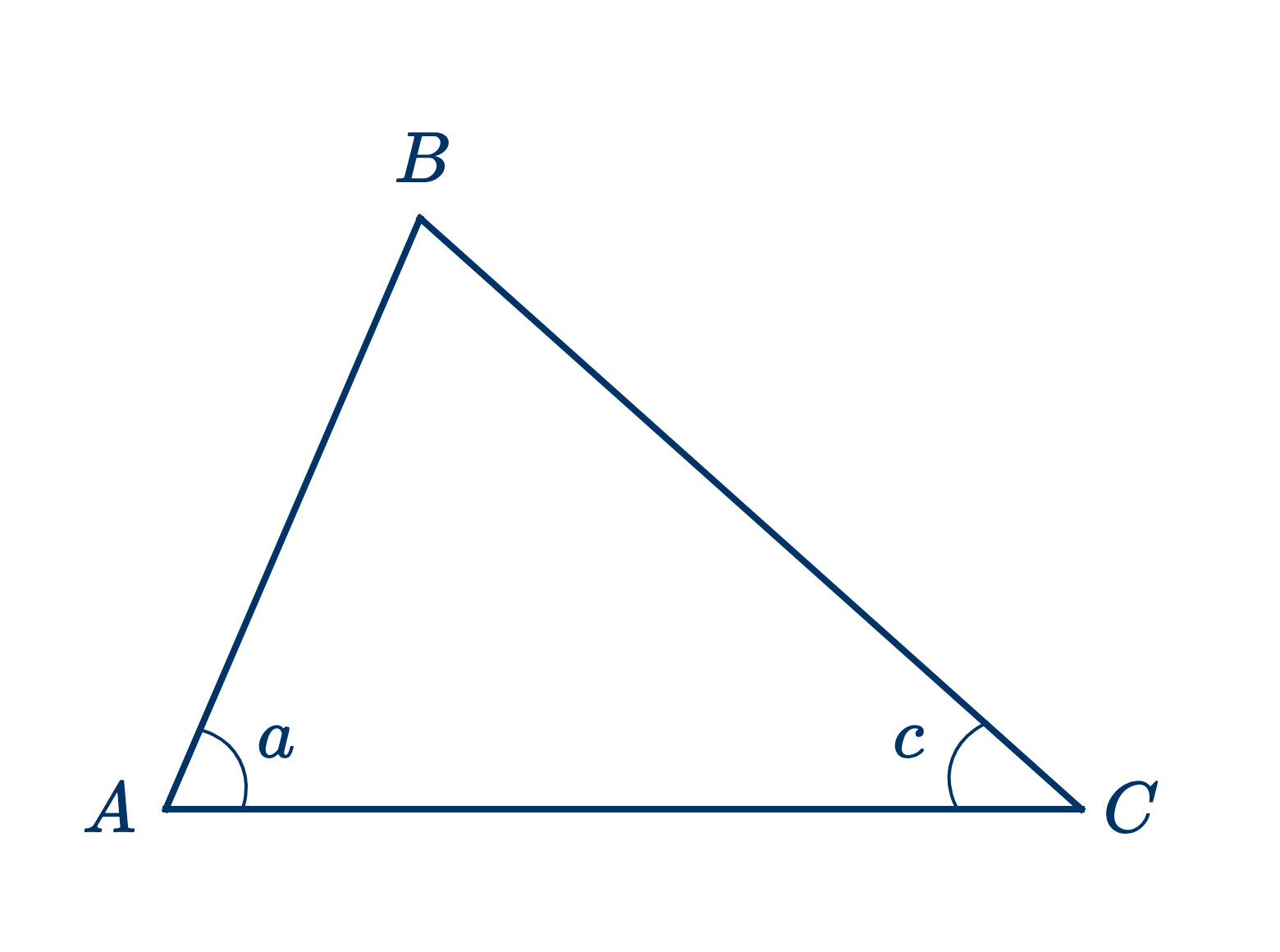
Дано: в треугольнике $ABC$ угол $a>c$.
Доказать, что сторона $BC>AB$.

$AB$ может быть равна, больше или меньше $BC$.
Если $AB=BC$, тогда $c=a$. (см. теорему .)
Если $AB>BC$, тогда $c>a$. (см. теорему .)
Но оба утверждения противоречат условию, что $a>c$.
Поэтому $AB < BC$.
Q.E.D.

• Теорема.

  Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника, то такие треугольники равны.

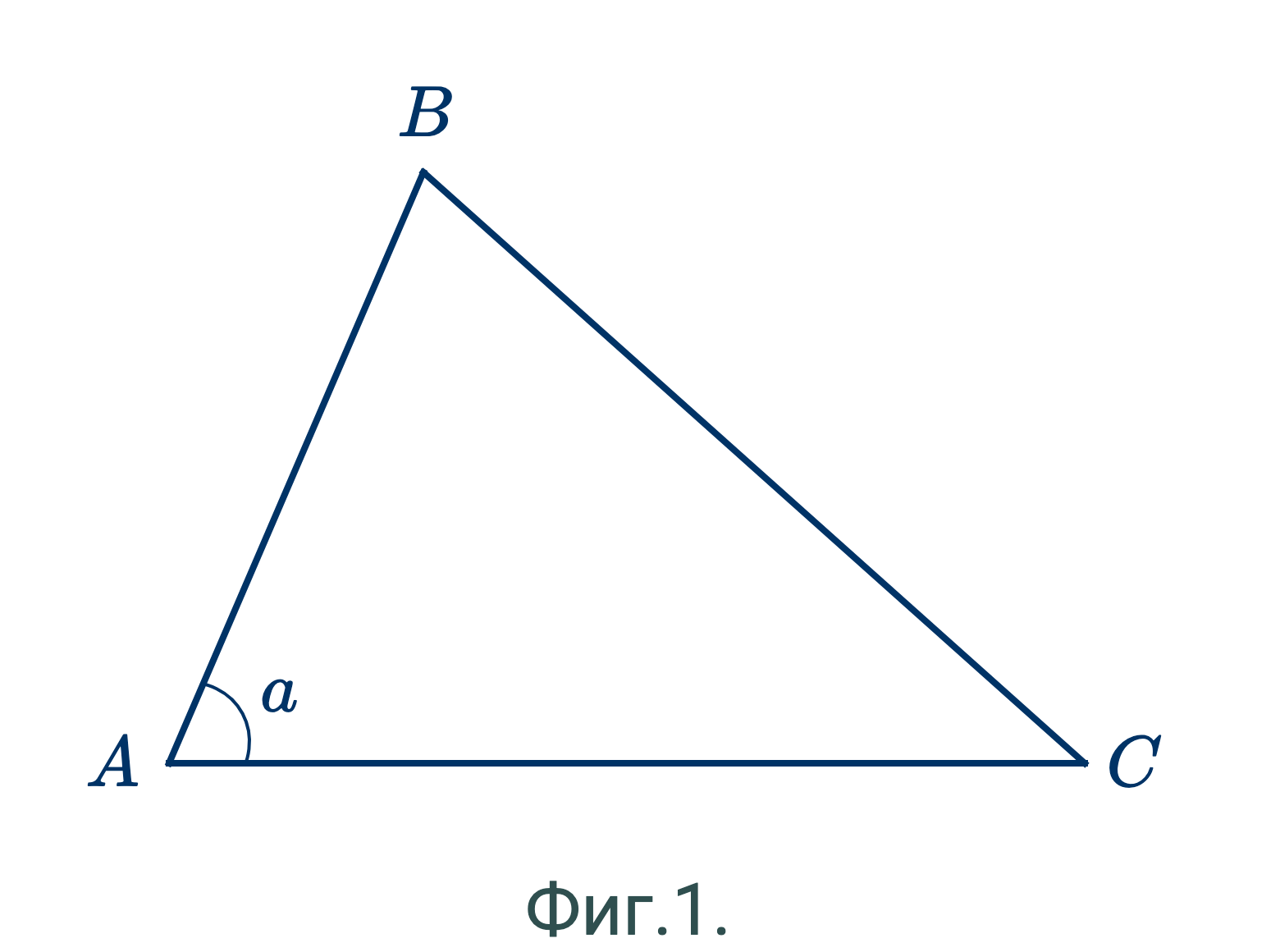
Дано: $AB, AC$ и $a$ треугольника $ABC$ соответственно равны $A'B', A'C'$ и $a'$ треугольника $A'B'C'$.
Доказать, что эти два треугольника равны.

Наложим $ABC$ на $A'B'C'$ так, чтобы $AB$ совпала с равной ей $A'B'$.
Тогда, так как $a=a'$, сторона $AC$ пойдет вдоль стороны $A'C'$.
Далее, вследствие того, что $AC=A'C'$, точка $C$ упадет в точку $C'$.
Тогда $BC$ совпадет с $B'C'$. (см. акс. прямой.)
И так как треугольники полностью совпали, то они равны.
Q.E.D.

Построение.

Построить угол при данной вершине $A'$ и на данной стороне $A'B'$, равный данному углу $BAC$ при вершине $A$.

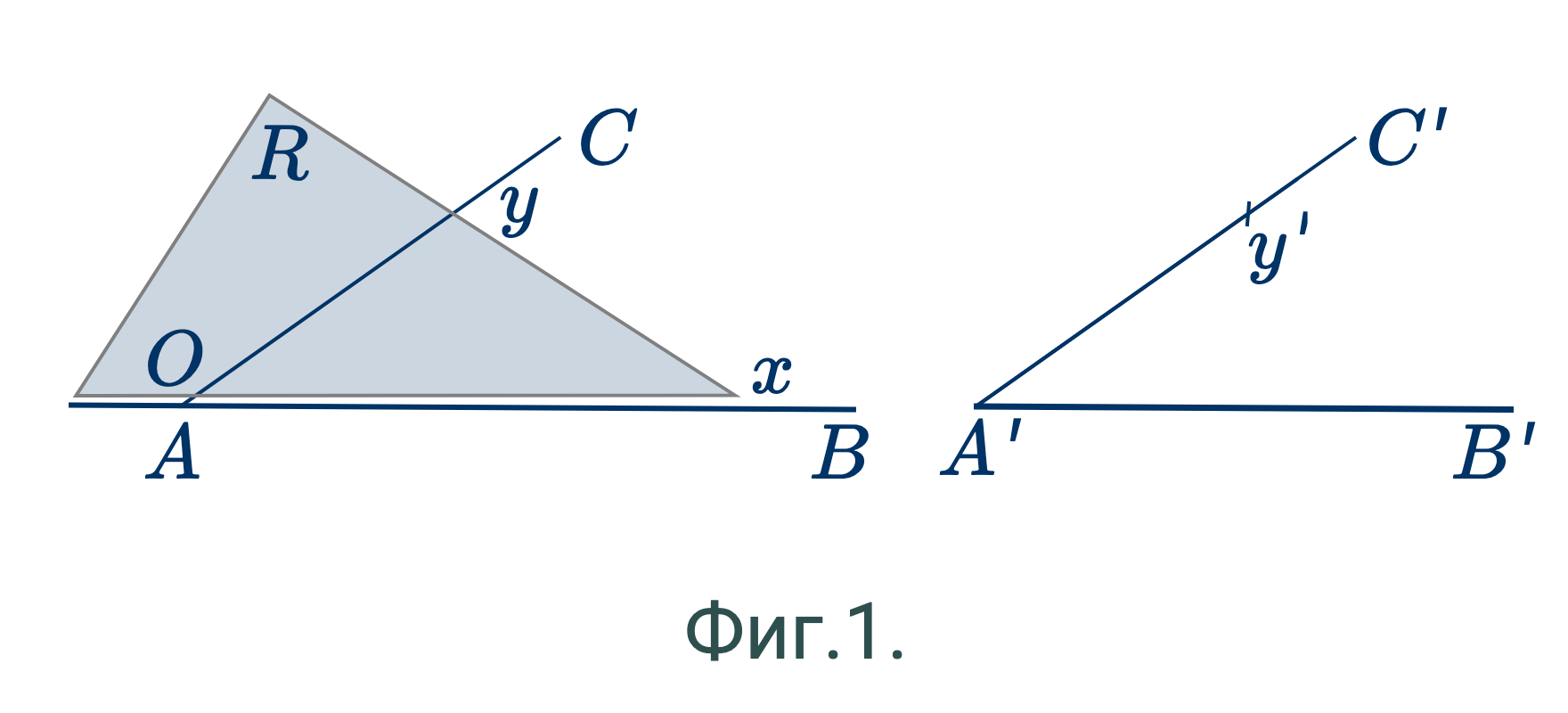
Первый способ. (Фиг.1.) — Наложим наугольник $R$ так, чтобы одна сторона его пошла по прямой $AB$. Отметим $y$ на другой стороне наугольника, как место его пересечения с прямой $AC$. Положение точки $A$ на наугольнике отметим буквой $O$. Проведем $Oy$ при помощи линейки. Тогда угол $BAC$ будет представлен углом $xOy$ наугольника. Теперь наложим наугольник так, чтобы $O$ совпала с $A'$, а сторона $Ox$ пошла вдоль $A'B'$; тогда угол $xOy$ перенесется с наугольника на бумагу, и мы получим угол $B'A'C'$. Итак, $\angle B'A'C'=\angle BAC$.

Вопрос.

Какие геометрические и какие общие аксиомы следует применить?

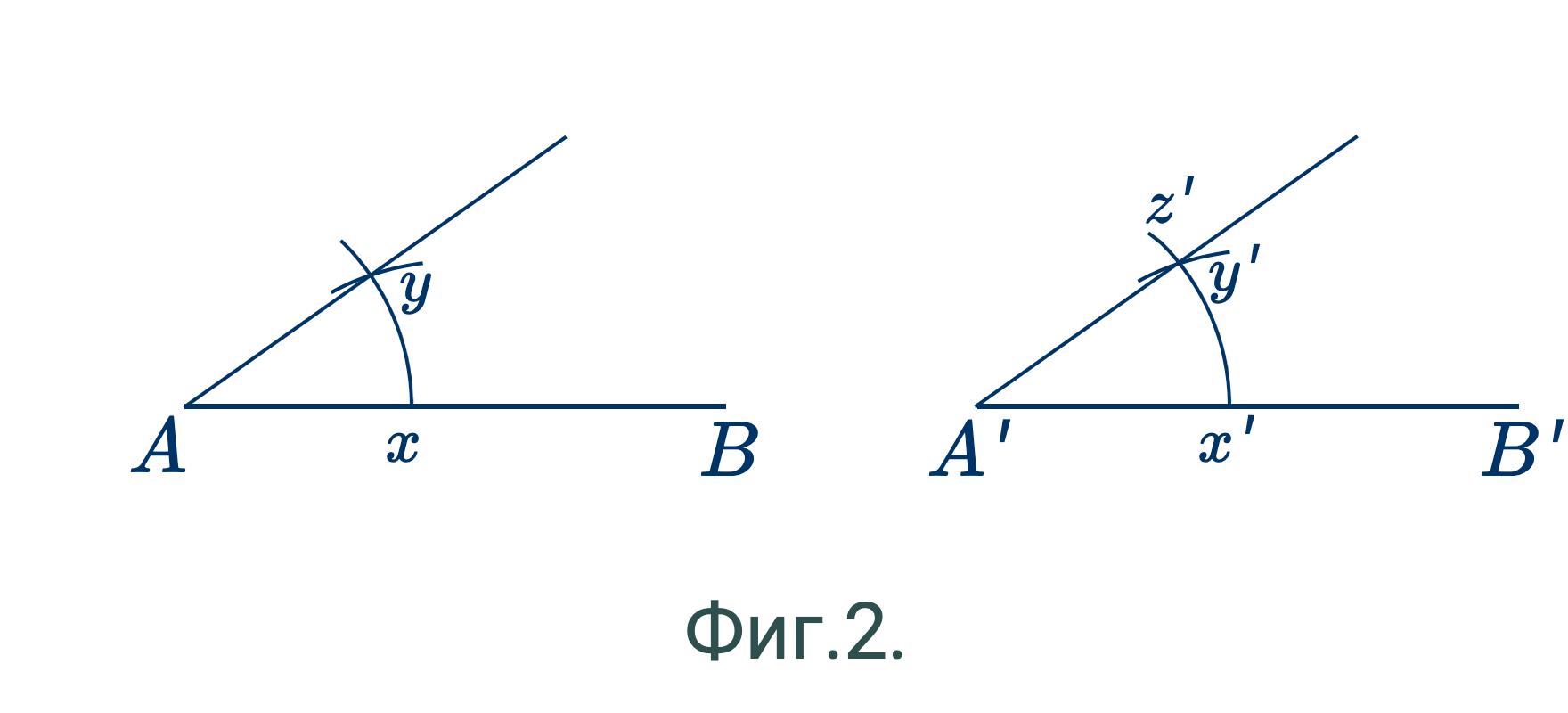
Второй способ. (Фиг.2.) — Из точки $A$, как из центра, соответствующим радиусом опишем дугу $xy$. Из точки $A'$, как из центра, тем же радиусом опишем дугу $x'z'$. Взяв теперь отрезок $xy$ прямой за радиус, опишем из $x'$, как из центра, дугу, пересекающую $x'z'$ в точке $y'$. Проведем $y'A'$. Угол $y'A'B'$ и есть искомый угол.

Замечание.

Это не может быть строго доказано раньше теоремы .

Построение.

Построить треугольник, у которого две стороны и заключенный между ними угол соответственно равны двум отрезкам $a$ и $b$ и данному углу $x$.

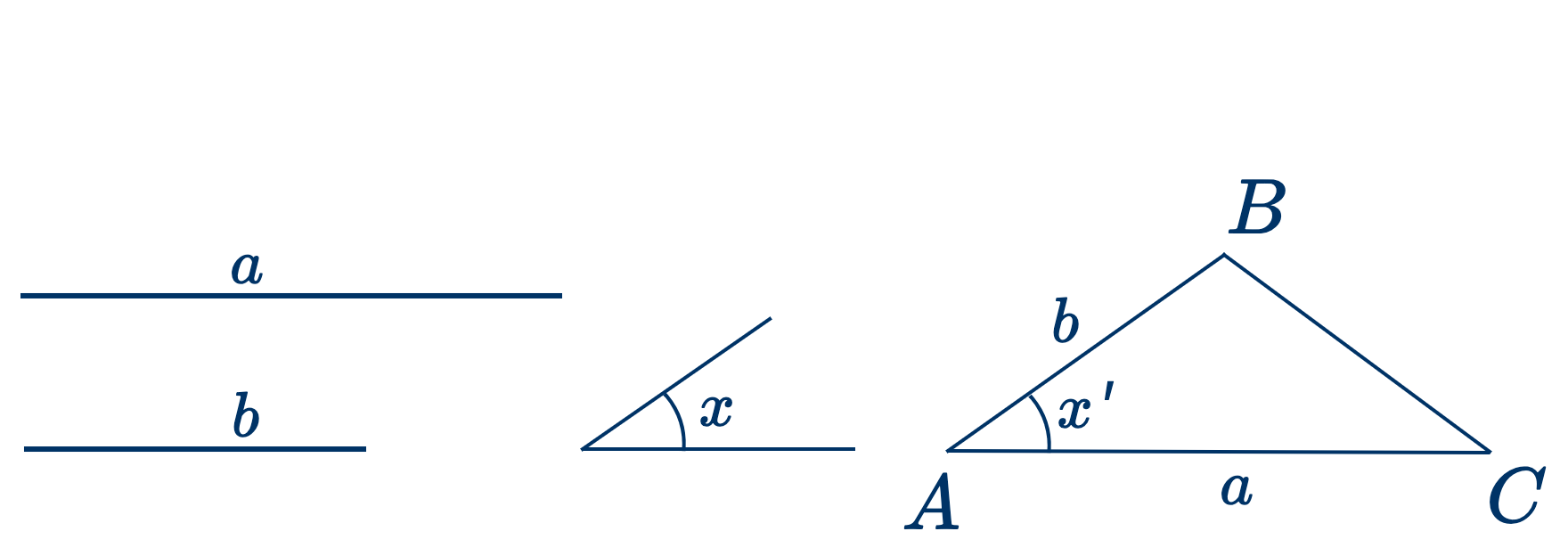
Отложите $AC=a$. Постройте $x'=x$ (см. § 6.) Отложите $AB=b$. Проведите $BC$. $ABC$ есть требуемый треугольник, у которого две стороны и заключенный между ними угол построены как требовалось.

• Теорема.

  Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

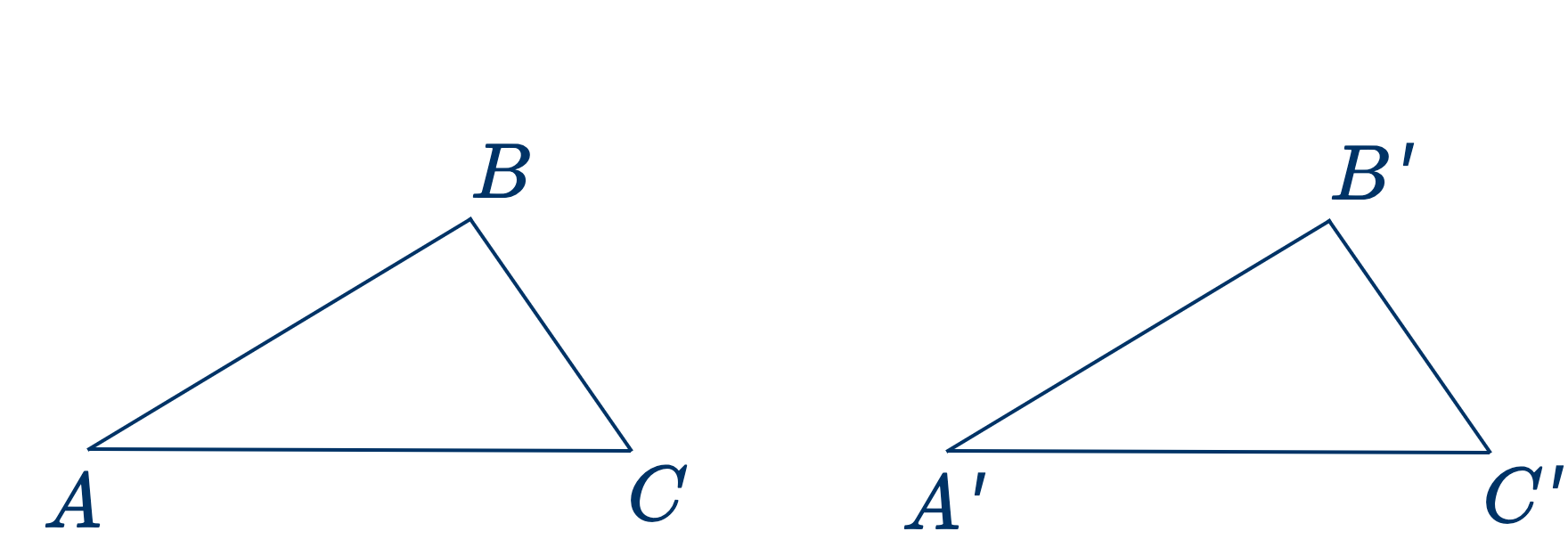
Дано: в двух треугольниках $ABC$ и $A'B'C': AB=A'B'$, а углы $A$ и $B$ соответственно равны углам $A'$ и $B'$
Доказать, что эти два треугольника равны.

Наложим $ABC$ на $A'B'C'$ так, чтобы $AB$ совпала с равной ей $A'B'$.
Тогда, $AC$ пойдет вдоль $A'C'$, также как и $BC$ вдоль $B'C'$. (Вследствие того, что углы $A$ и $B$ соответственно равны $A'$ и $B'$.)
Отсюда $C$ должна упасть где-нибудь на прямую $A'C'$ и также где-нибудь на прямую $B'C'$.
Поэтому она должна упасть в точку их пересечения $C'$.
И так как треугольники полностью совпали, то они равны.
Q.E.D.

Следствие.

Если сторона и любые два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны.

Указание.

Сведите к предыдущей теореме. (см. следствие теоремы .)

Вопрос.

Сколько раз вы встретите в треугольниках $ABC$ и $A'B'C'$ равную сторону и два соответственно расположенных равных угла? Начертите два треугольника, имеющих равную сторону и два равных угла, хотя и не одинаково расположенных.

Определение.

В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой; две другие стороны называются перпендикулярными сторонами (их также называют греческим термином катет).

Следствие.

Два прямоугольных треугольника равны, если гипотенуза и острый угол одного соответственно равны гипотенузе и острому углу другого.

Следствие.

Два прямоугольных треугольника равны, если катет и острый угол одного соответственно равны катету и острому углу другого.

Построение.

Если два угла треугольника равны данным углам $a$ и $b$, то найдите третий угол.

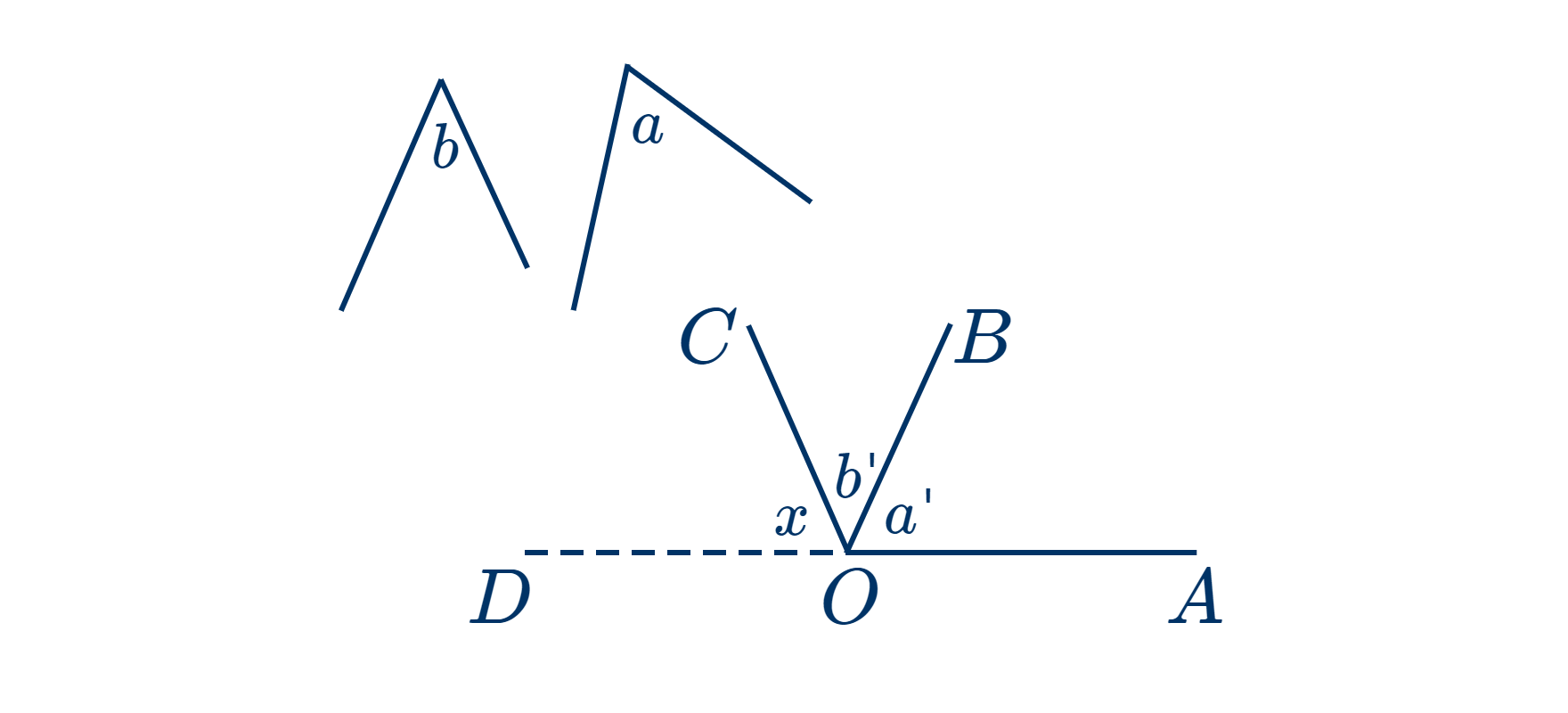
На прямой $OA$ постройте угол $a'=a$, а на прямой $OB$ при той же вершине $O$ постройте $b'=b$. Продолжите $OA$ до точки $D$; получится угол $x$. Это и есть искомый угол. Докажите это (см. следствие теоремы .)

Построение.

Построить треугольник, у которого сторона и два угла соответственно равнялись бы данному отрезку $m$ и двум углам $a$ и $b$.

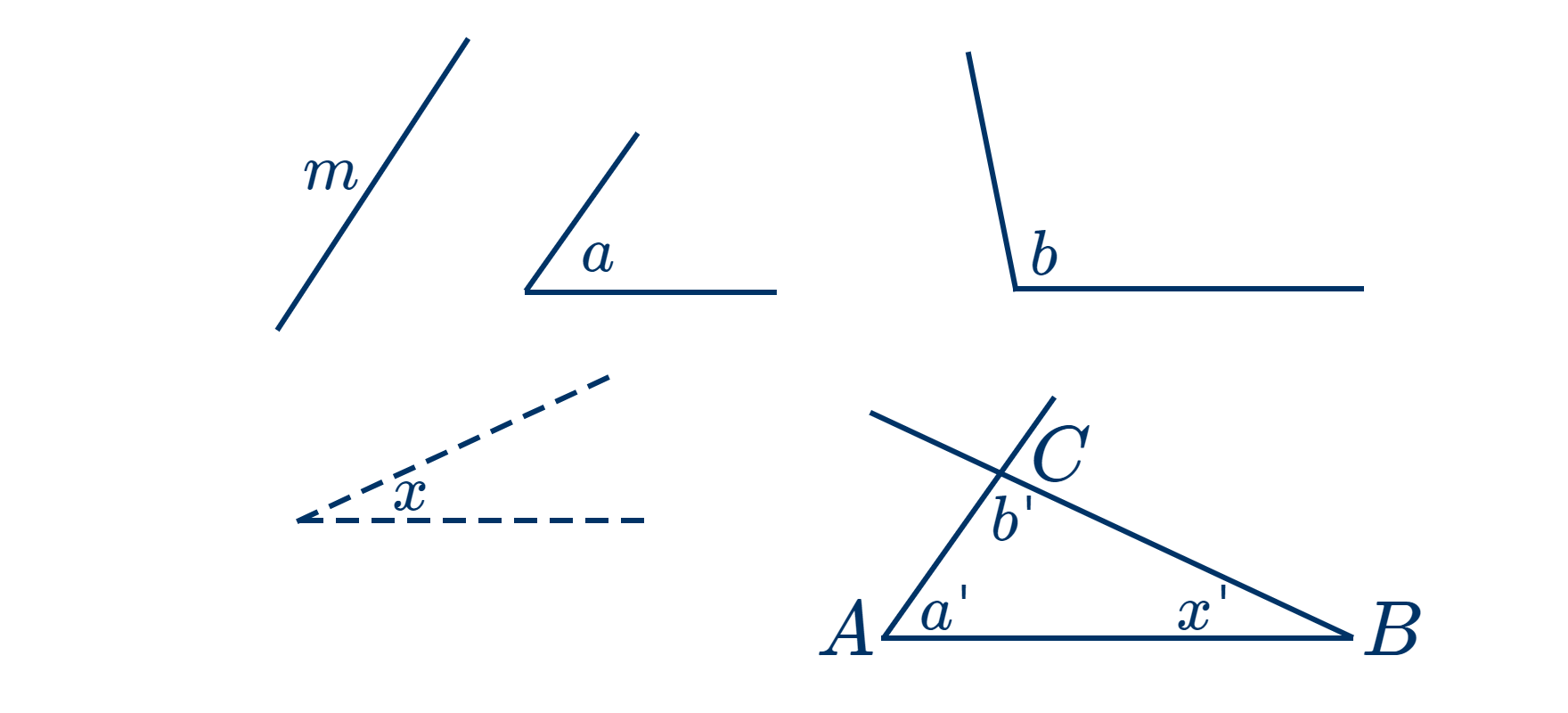
Найдите (пользуясь предыдущим построением) $x$, третий угол треугольника.

Начертите отрезок $AB$, равный $m$, и постройте при точках $A$ и $B$ два угла, прилежащих к этой стороне и равных любым двум из углов $a$, $b$, $x$. Если начерченные стороны этих углов продолжить, то они пересекутся; точкой их пересечения будет $C$. $ABC$ есть искомый треугольник, так как $AB=m$ по построению, а углы $a'$ и $b'$ равны $a$ и $b$ по построению или на основании следствия.

• Теорема.

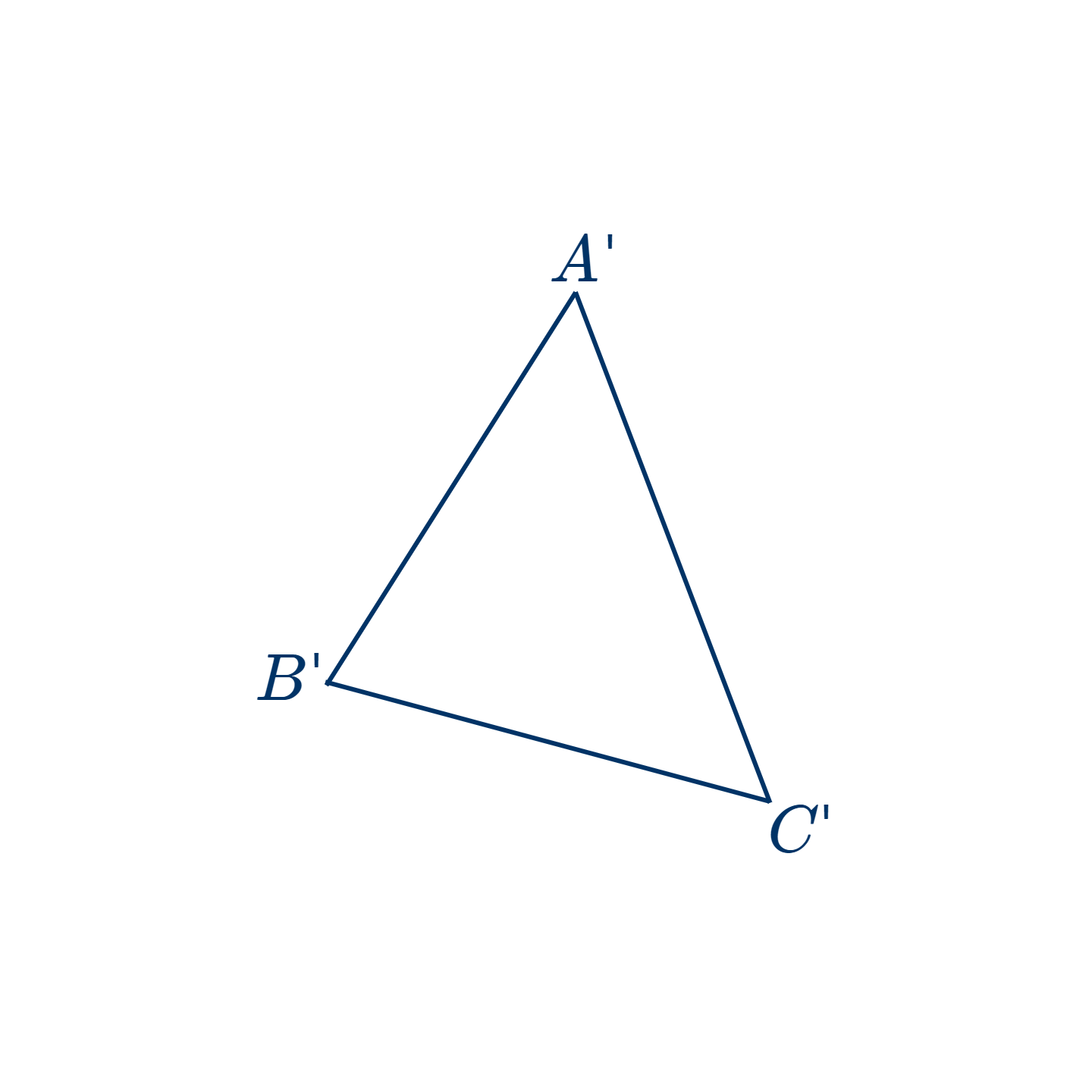
  Если три стороны одного треугольника соответственно равны трем сторонам другого, то эти треугольники равны.

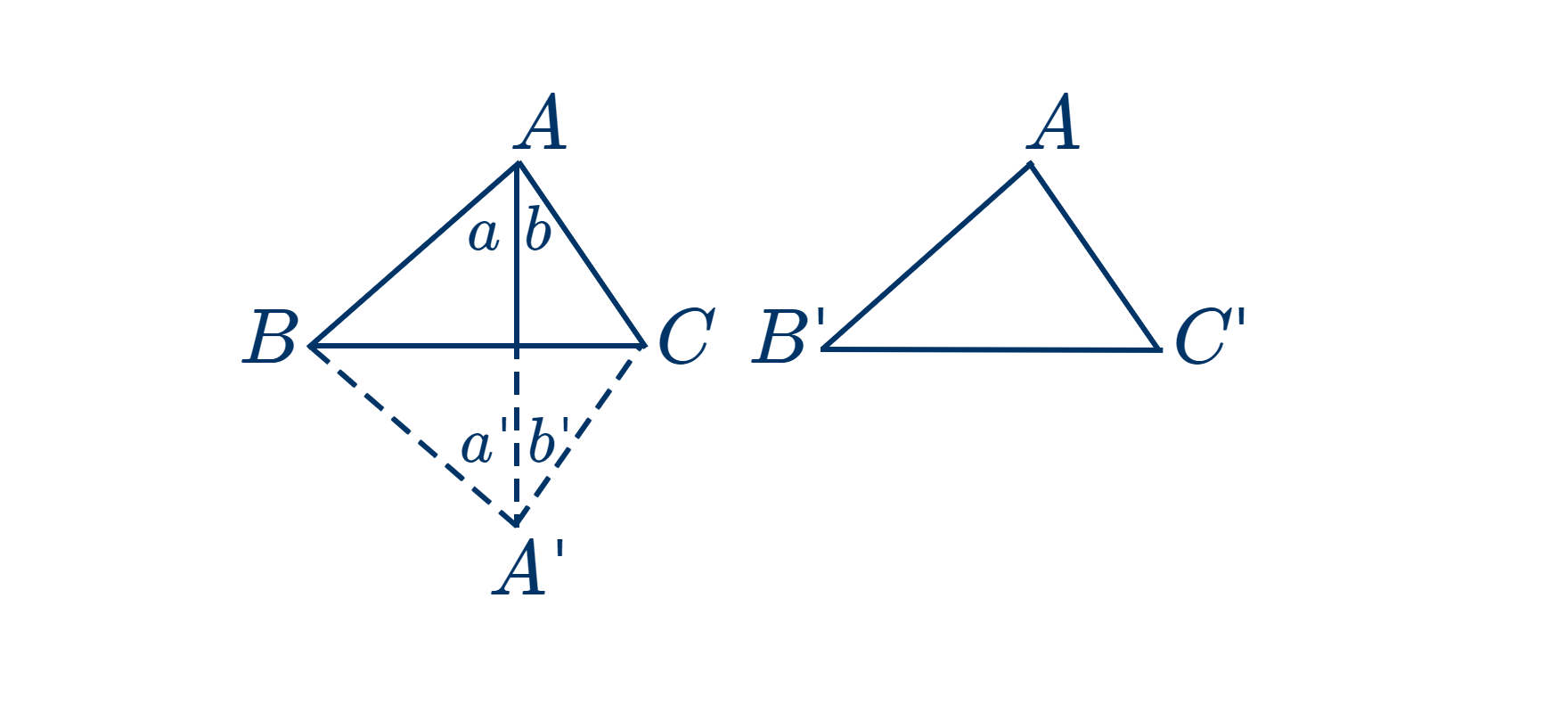
Дано: в двух треугольниках $ABC$ и $A'B'C': AB=A'B'$, а углы $A$ и $B$ соответственно равны углам $A'$ и $B'$
Доказать, что эти два треугольника равны.

Наложим $ABC$ на $A'B'C'$ так, чтобы $AB$ совпала с равной ей $A'B'$.
Тогда, $AC$ пойдет вдоль $A'C'$, также как и $BC$ вдоль $B'C'$. (Вследствие того, что углы $A$ и $B$ соответственно равны $A'$ и $B'$.)
Отсюда $C$ должна упасть где-нибудь на прямую $A'C'$ и также где-нибудь на прямую $B'C'$.
Поэтому она должна упасть в точку их пересечения $C'$.
И так как треугольники полностью совпали, то они равны.
Q.E.D.

Построение.

Построить треугольник, у которого три стороны были бы равны данным отрезкам $a$, $b$ и $c$.

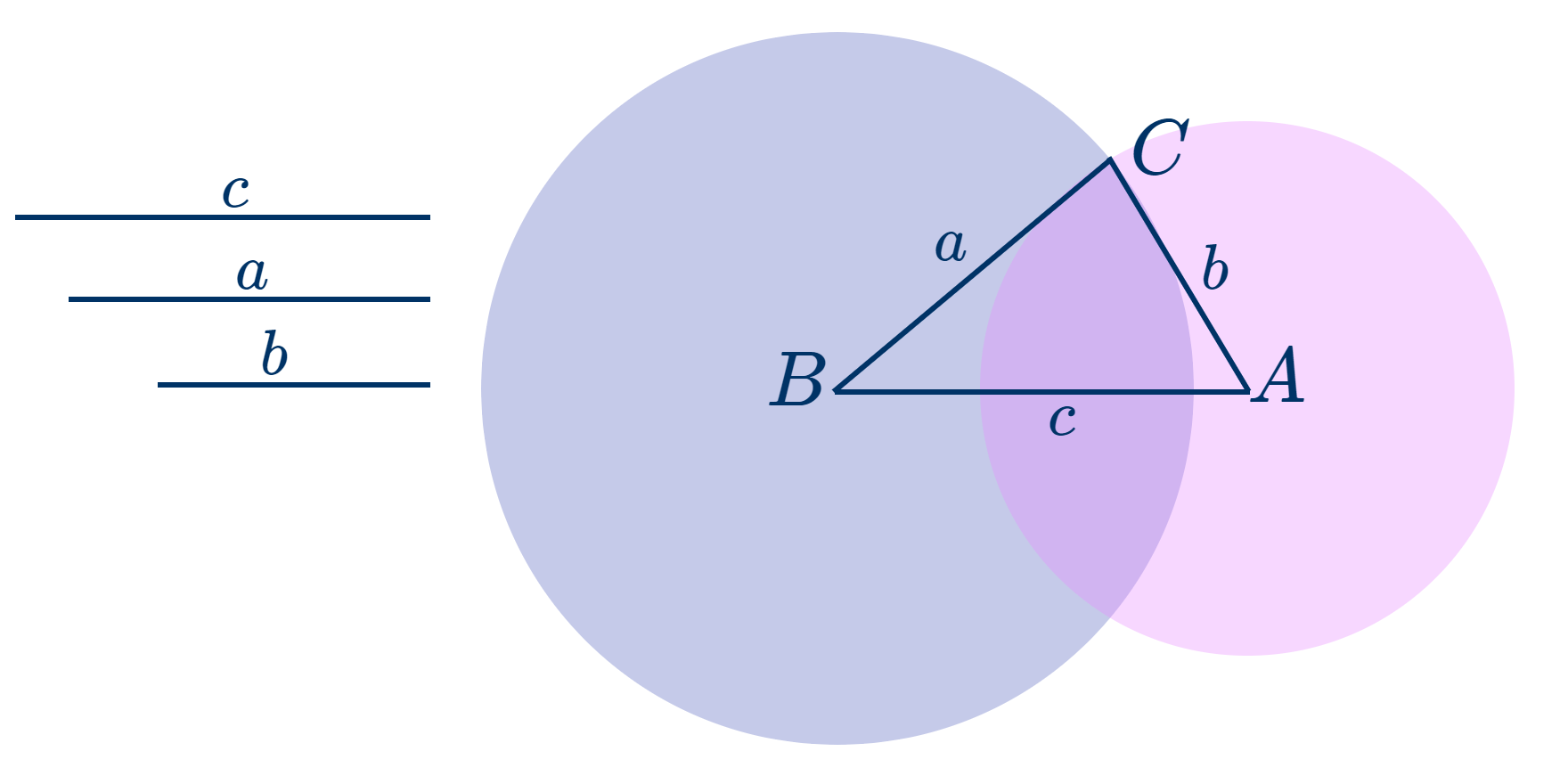
• Теорема.

  Из точки прямой можно провести один и только один перпендикуляр (по одну сторону данной прямой).

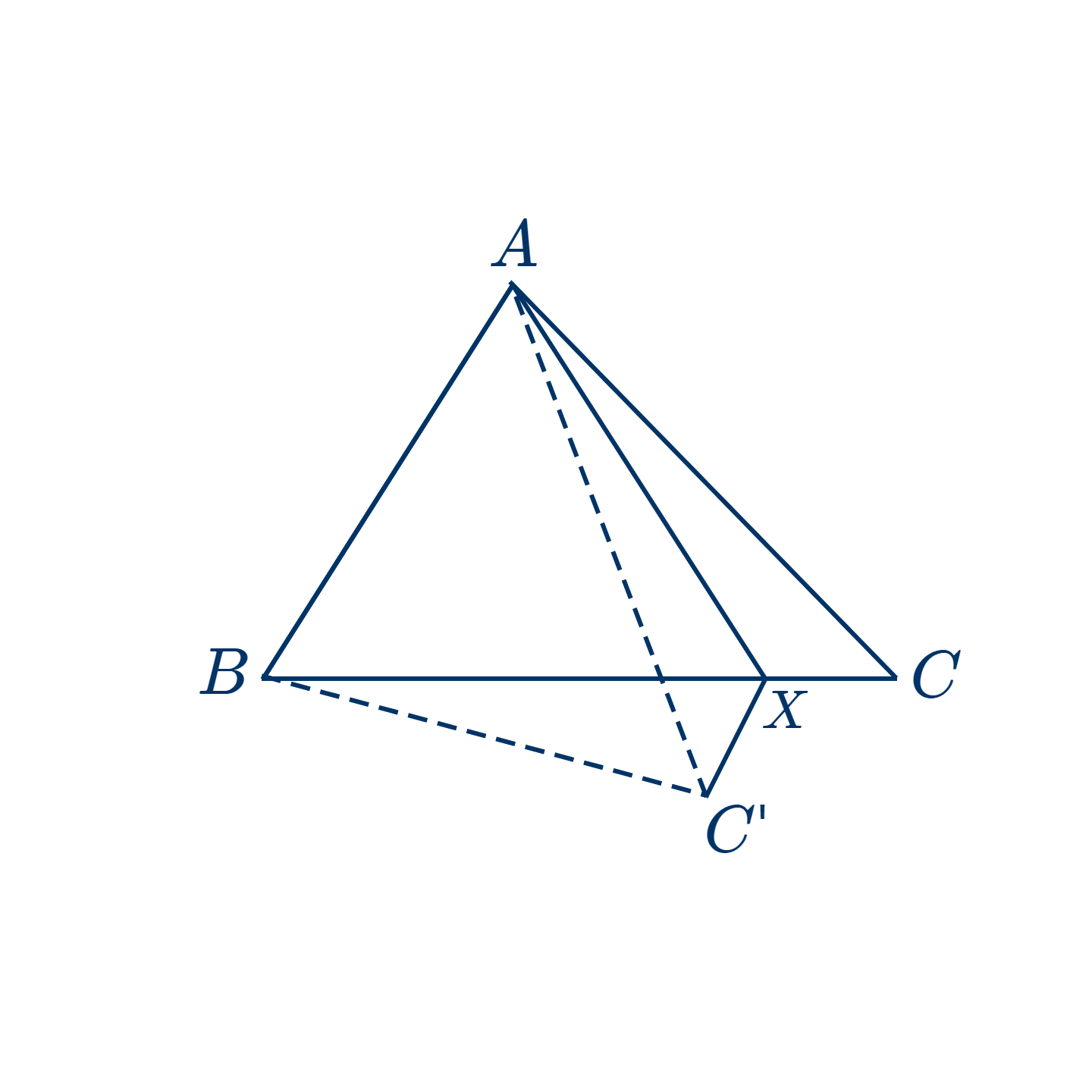
• Теорема.

  Из точки прямой можно провести один и только один перпендикуляр (по одну сторону данной прямой).

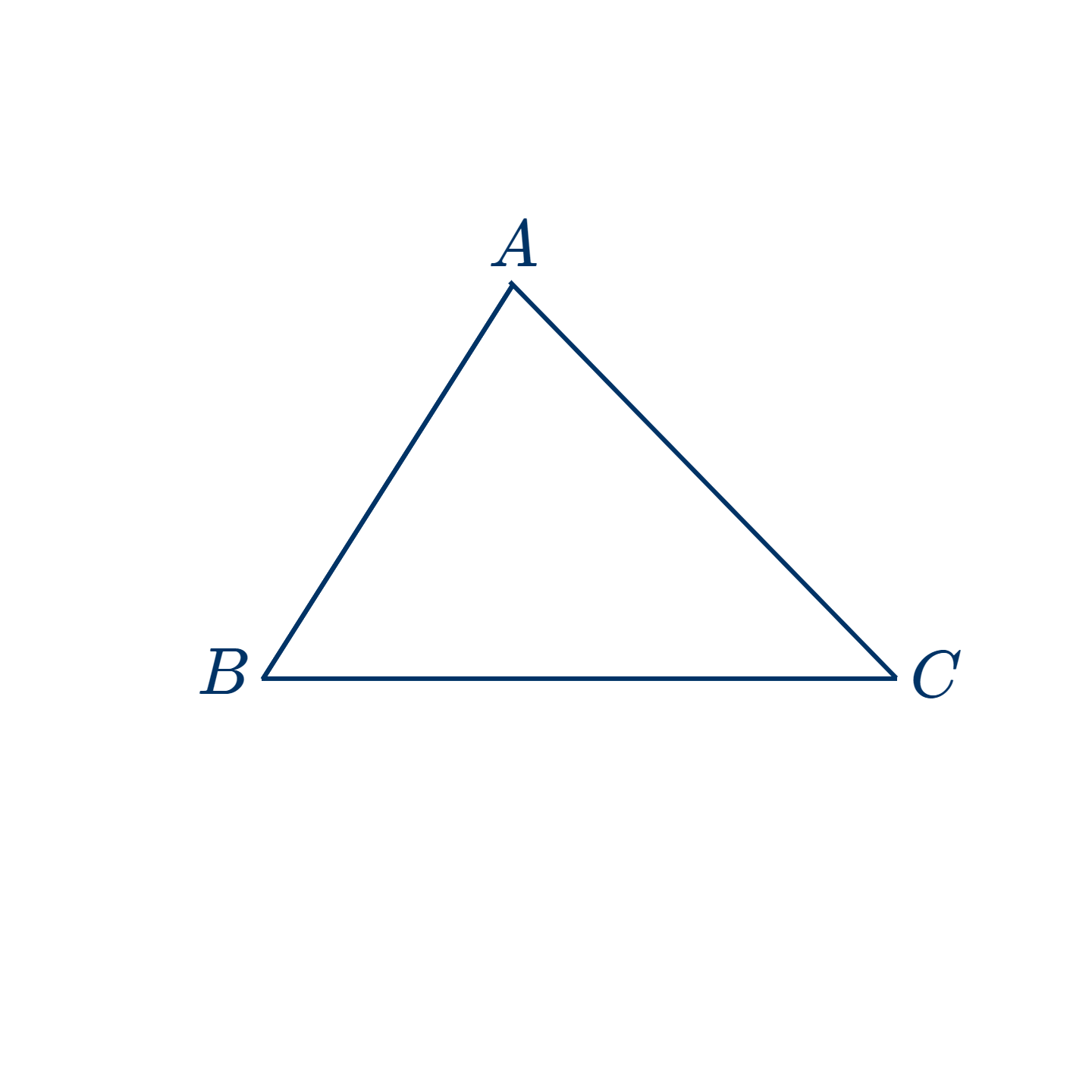
Построение.

Из точки прямой можно провести один и только один перпендикуляр (по одну сторону данной прямой).

← Читать дальше