Фигуры, составленные из прямых линий

Определение.: Углом называется фигура, составленная из двух прямых линий, выходящих из одной точки.

Замечание.: С этого момента обусловимся, что всякая точка на чертеже рисоваться не будет, но лишь будет отмечена соответствующей заглавной буквой.

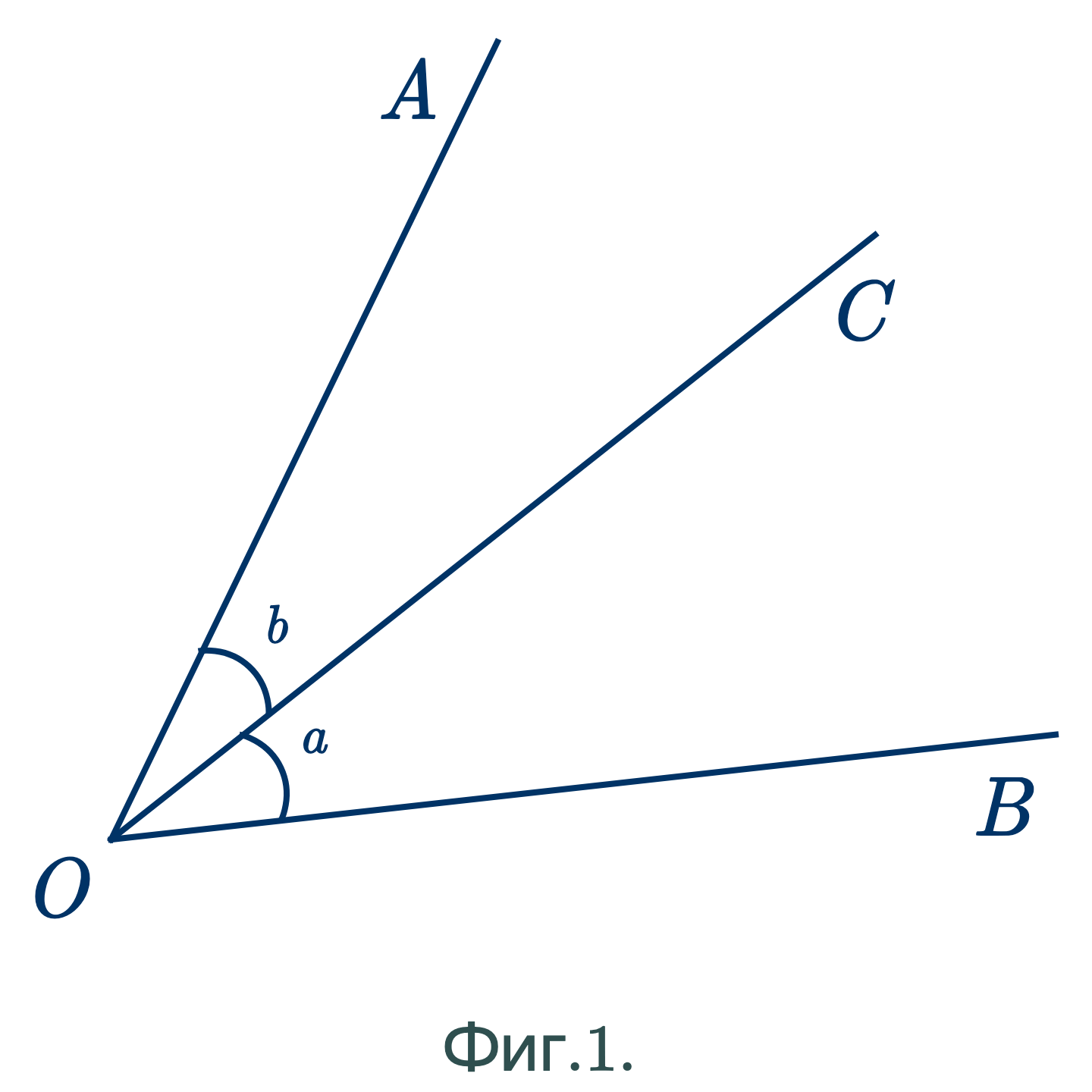
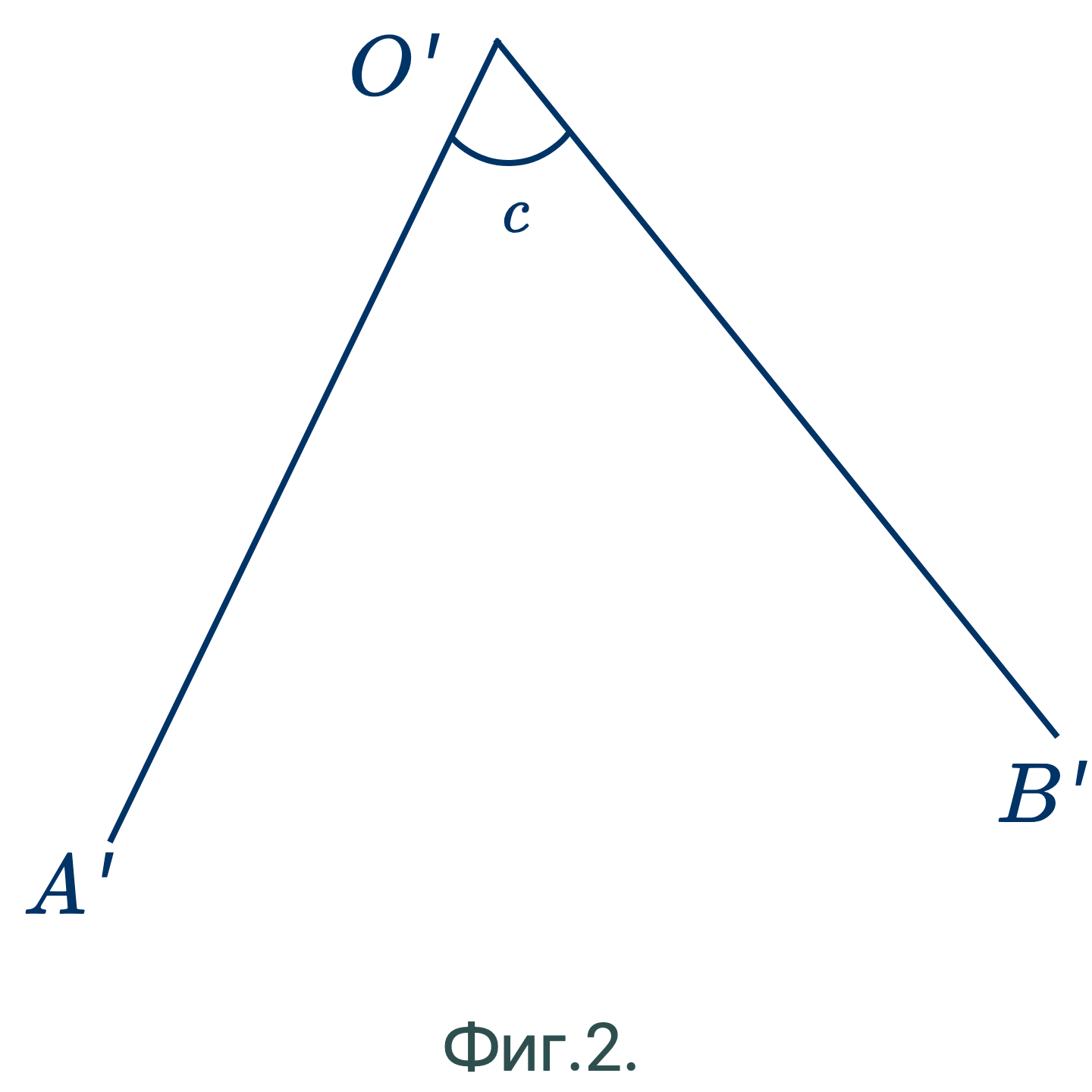
Обозначим углы буквами $a$ и $b$ в фиг. 1 и буквой $c$ в фиг. 2.

Можно ставить и три буквы таким образом: по букве на каждой стороне и одну при вершине угла; эта последняя читается между двумя другими, как, например, $\angle AOC$, $\angle BOC$ и $\angle AOB$ в фиг. 1 и $\angle A'O'B'$ в фиг. 2.

Если при точке имеется только один угол, то он может быть обозначен одной буквой, как, например, $O'$ в фиг. 2.

Определение.: Углы, имеющие общую вершину и общую сторону, как, например, $a$ и $b$, называются прилежащими.

Определение.: Два угла равны, если они при наложении совпадают. Вообще, две фигуры равны, если они при наложении совпадают.

Предположим, что мы накладываем угол $AOB$ на угол $A'O'B'$ так, что $O$ падает на $O'$, а сторона $OA$ идет по стороне $O'A'$; если сторона $OB$ также пойдет по $O'B'$, то углы будут равны, какова бы ни была длина каждой из их сторон.

Определение.: Если прямая, исходя из любой точки другой прямой, образует два равных прилежащих угла, то каждый из них называется прямым углом, а каждая из прямых называется перпендикуляром.

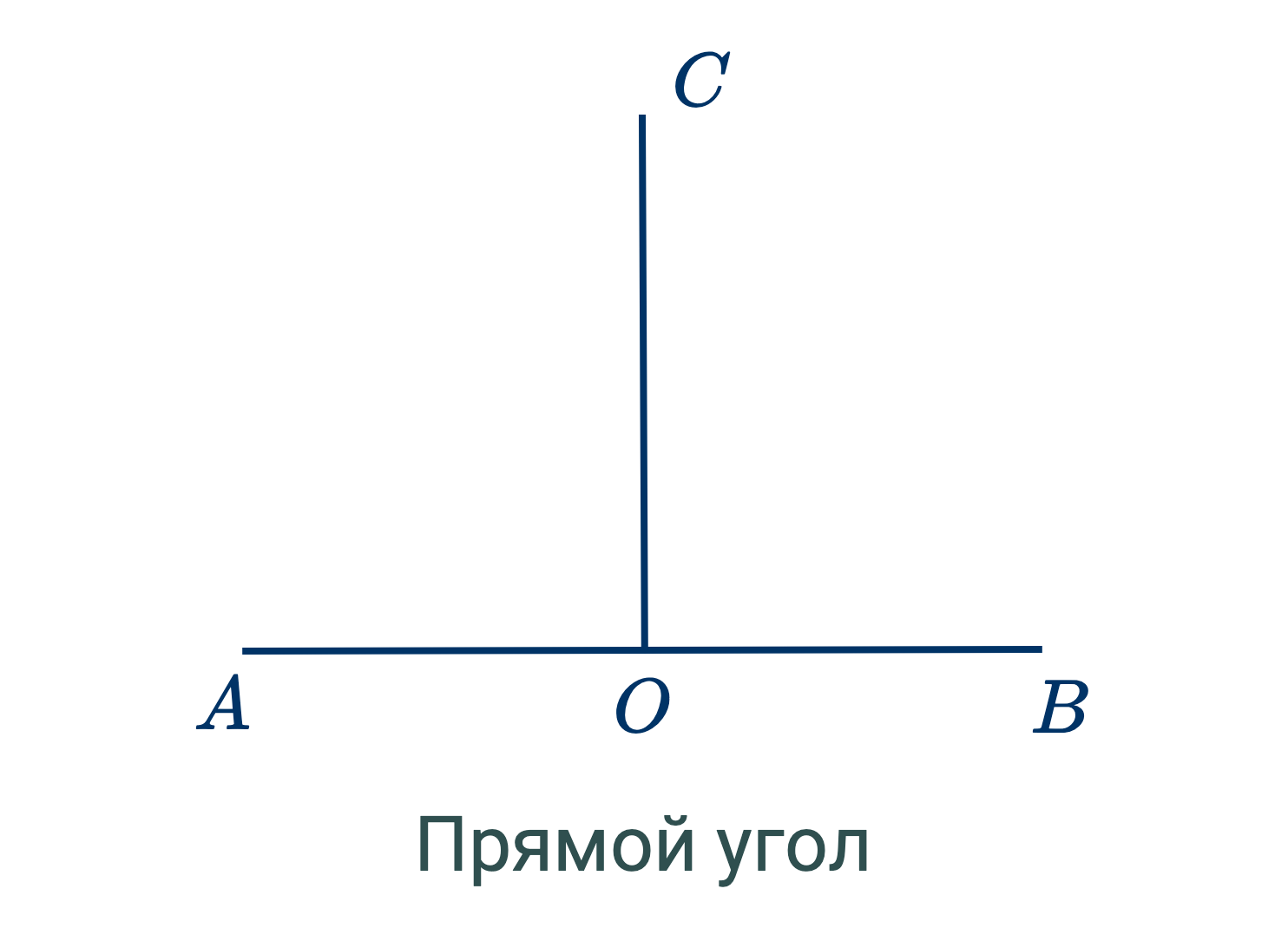
Таким образом, если углы $AOC$ и $COB$ равны, они будут прямые углы и $CO$ – перпендикуляр к $AB$.
Если прямая линия есть перпендикуляр к другой прямой, точка ее пересечения со второй линией называется основанием перпендикуляра.

Определение.: Острый угол меньше прямого, тупой больше прямого.

Теорема.

Из точки прямой можно провести один и только один перпендикуляр (по одну сторону данной прямой).

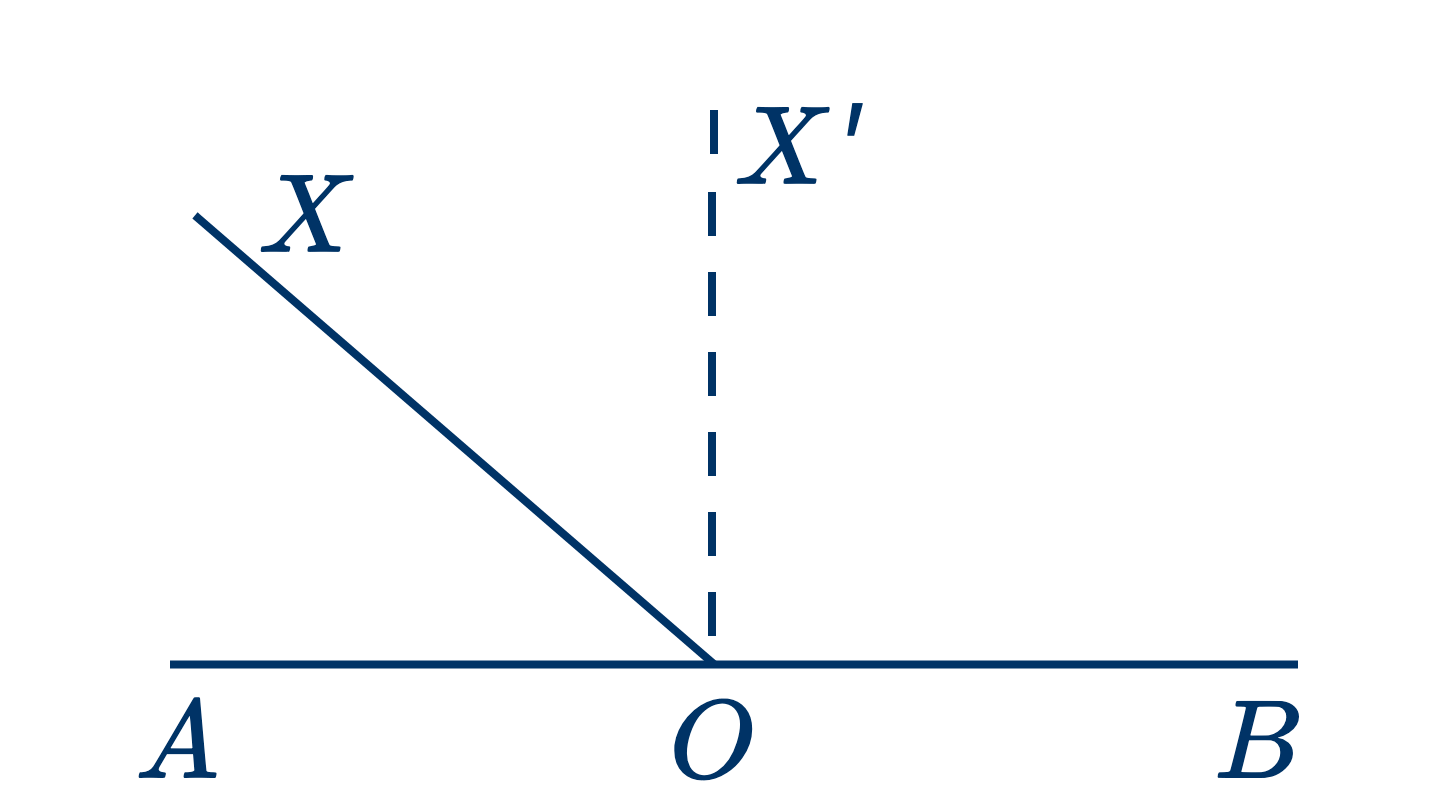
Дано: прямая линия $AB$ и какая-нибудь точка $O$ на ней. Доказать, что из точки $O$ можно провести один и только один перпендикуляр к прямой $AB$ (по одну сторону $AB$).

Положим, что прямая линия $OX$ вращается около точки $O$. акс. наложения.
В каждом из своих последовательных положений она образует с прямой $AB$ два различных угла, например: $XOA$ и $XOB$.
Если она переходит от положения $OA$ к положению $OB$, то меньший угол, $XOA$, непрерывно увеличивается, а другой, $XOB$, непрерывно уменьшается.
Поэтому $OX$ может занять одно и только одно положение, а именно $OX'$, когда углы станут равными. акс. 12.
Итак, к прямой $AB$ в точке $O$ можно провести один и только один перпендикуляр.
Q.E.D.

Вопрос.: Данное предложение применяется к плоскости чертежа. Можно ли провести другие прямые, перпендикулярные к $AB$ в точке $O$, вне плоскости?

Теорема.

Все прямые углы равны между собою.

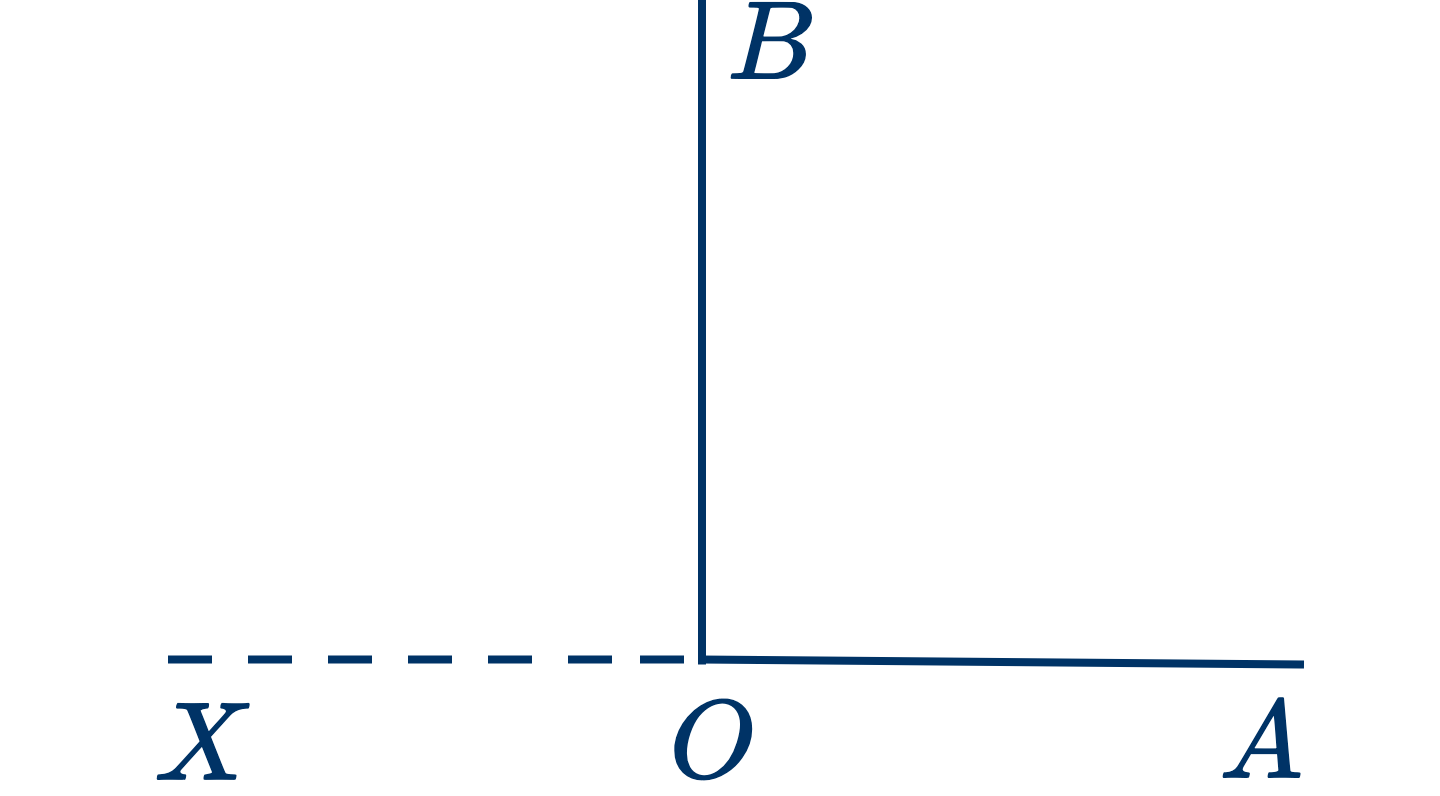
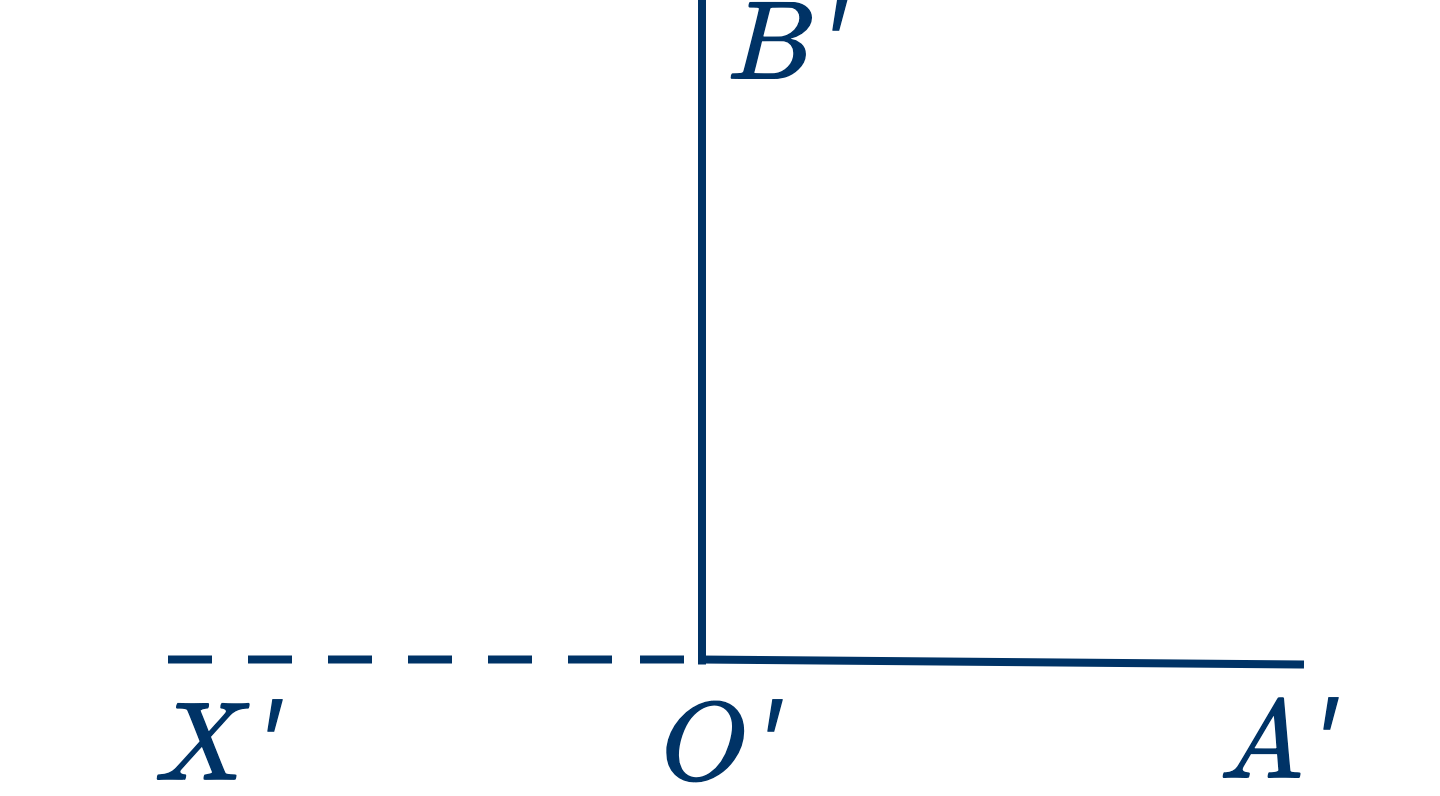
Дано: два прямых угла $AOB$ и $A'O'B'$
Доказать, что они равны.

Наложим $A'O'B'$ на $AOB$ так, чтобы вершина $O'$ упала на $O$, а точка $A'$ упала на одну из точек на прямой $OA$ или ее продолжение.
Тогда прямая $O'A'$ совпадет с $OA$, сколько бы мы их ни продолжали. акс. прямой.
Если бы $O'B'$ не пошла по $OB$, то получились бы две прямые $O'B'$ и $OB$, перпендикулярные к третьей в одной точке, что невозможно по теореме .
Поэтому $O'B'$ должна пойти по $OB$; тогда углы $A'O'B'$ и $AOB$ совпадут и, следовательно, они равны.
Q.E.D.

Определение.: Кругом называется плоская фигура, ограниченная линией, все точки которой находятся на равном расстоянии от точки внутри ее, называемой центром.

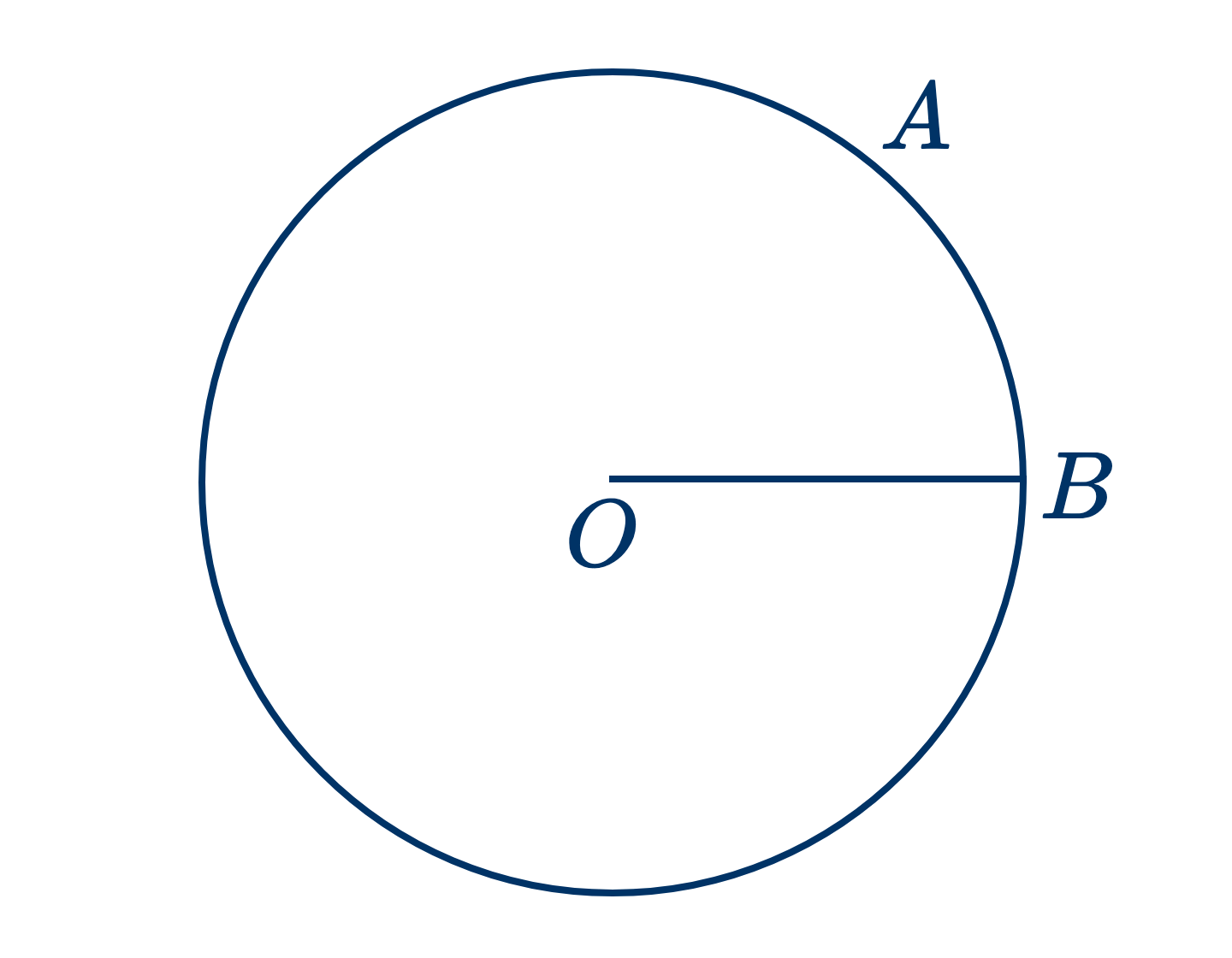
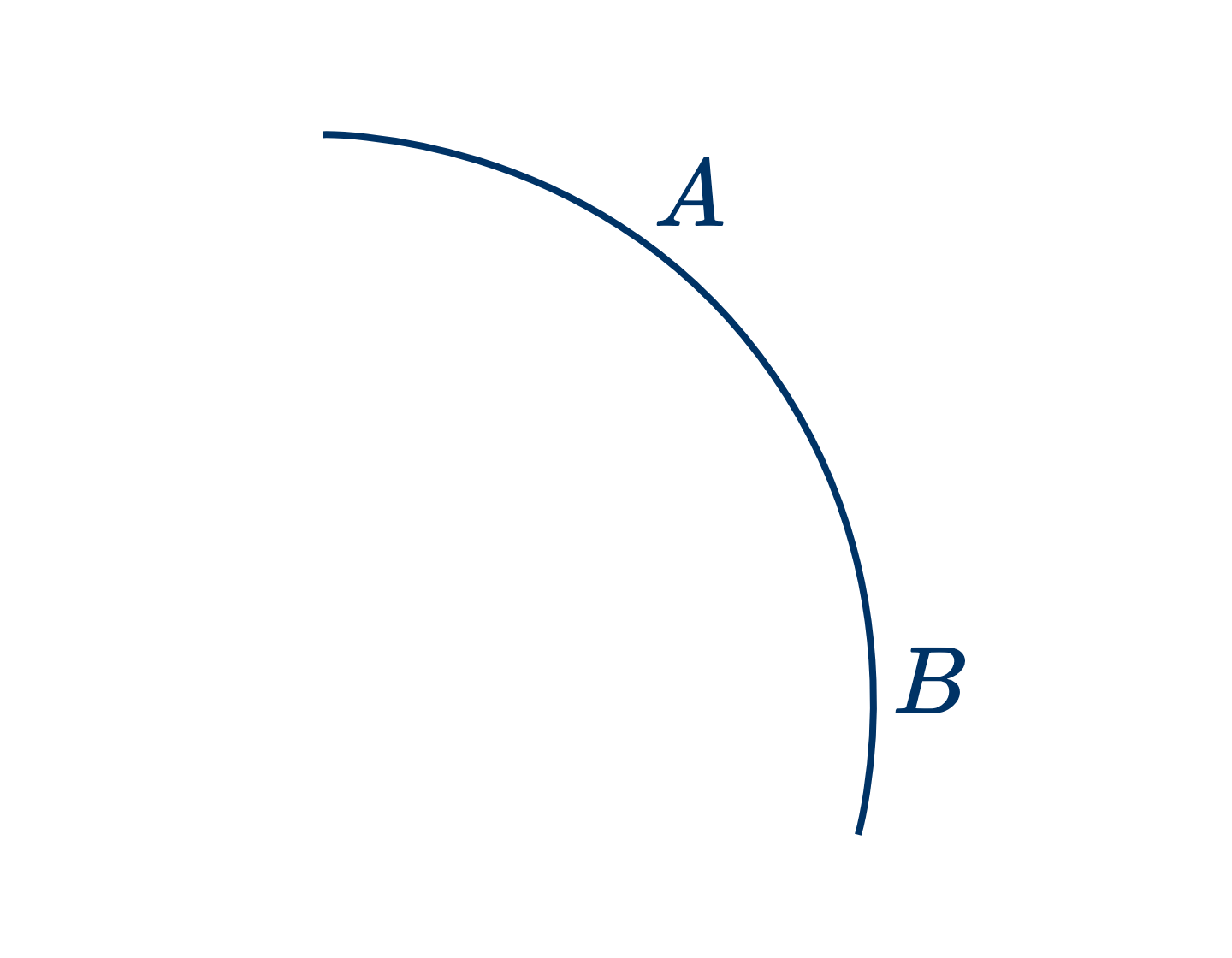
Определение.: Линия, ограничивающая круг, называется окружностью.
Всякая часть окружности называется дугой.
Все равные прямые, проведенные от центра к окружности (как $OB$), называются радиусами.

Построение.

Проведем перпендикуляр из любой точки прямой $AB$, например, $O$.

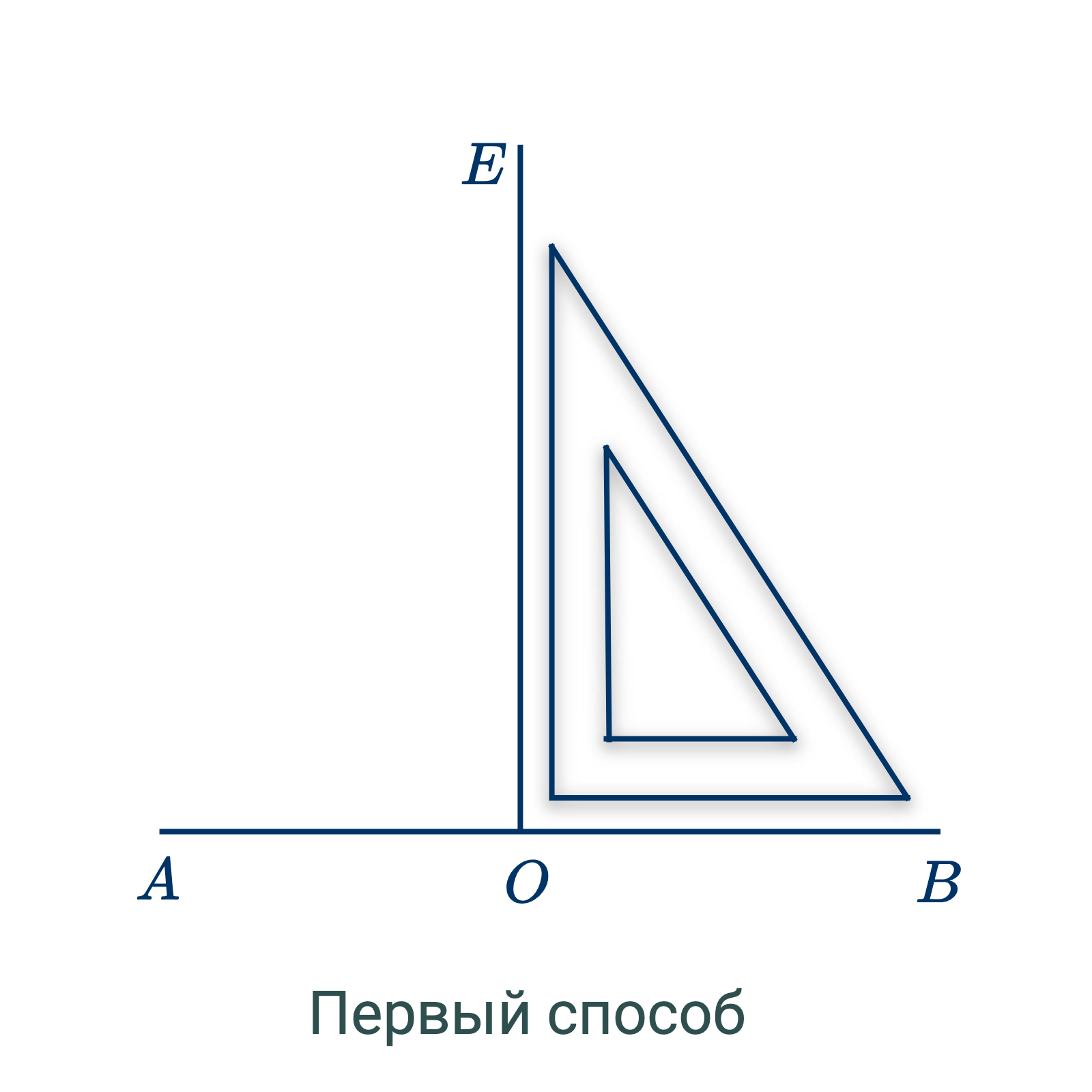
Первый способ. – Возьмем прибор, называемый наугольником, у которого один угол прямой, и поместим его так, чтобы вершина прямого угла прижалась в точку $O$, а одна из сторон его пошла по $AB$; затем проведем линию $OE$ вдоль другой стороны прямого угла наугольника. $OE$ будет требуемая прямая: во-первых, она проведена через точку $O$, и, во-вторых, она перпендикулярна к $AB$.

Замечание.: Вы должны видеть, что невозможно построить абсолютно точный чертеж, так как нет абсолютно точного наугольника и нельзя его наложить с абсолютной точностью. Более того, точки и линии, отмеченные карандашом, как бы ни был он заострен, не будут геометрическими точками и линиями, так как точки имеют некоторую величину и линии некоторую ширину. Чертежи только приближаются к требуемым идеальным линиям и точкам.
Но если бы практические приборы можно было сделать совершенными, то результаты построения были бы абсолютно точны. Поэтому о предыдущем построении мы можем сказать, что способ совершенен, но приборы никогда не могут быть таковыми.
Указанный способ обычно применяется чертежниками и столярами.

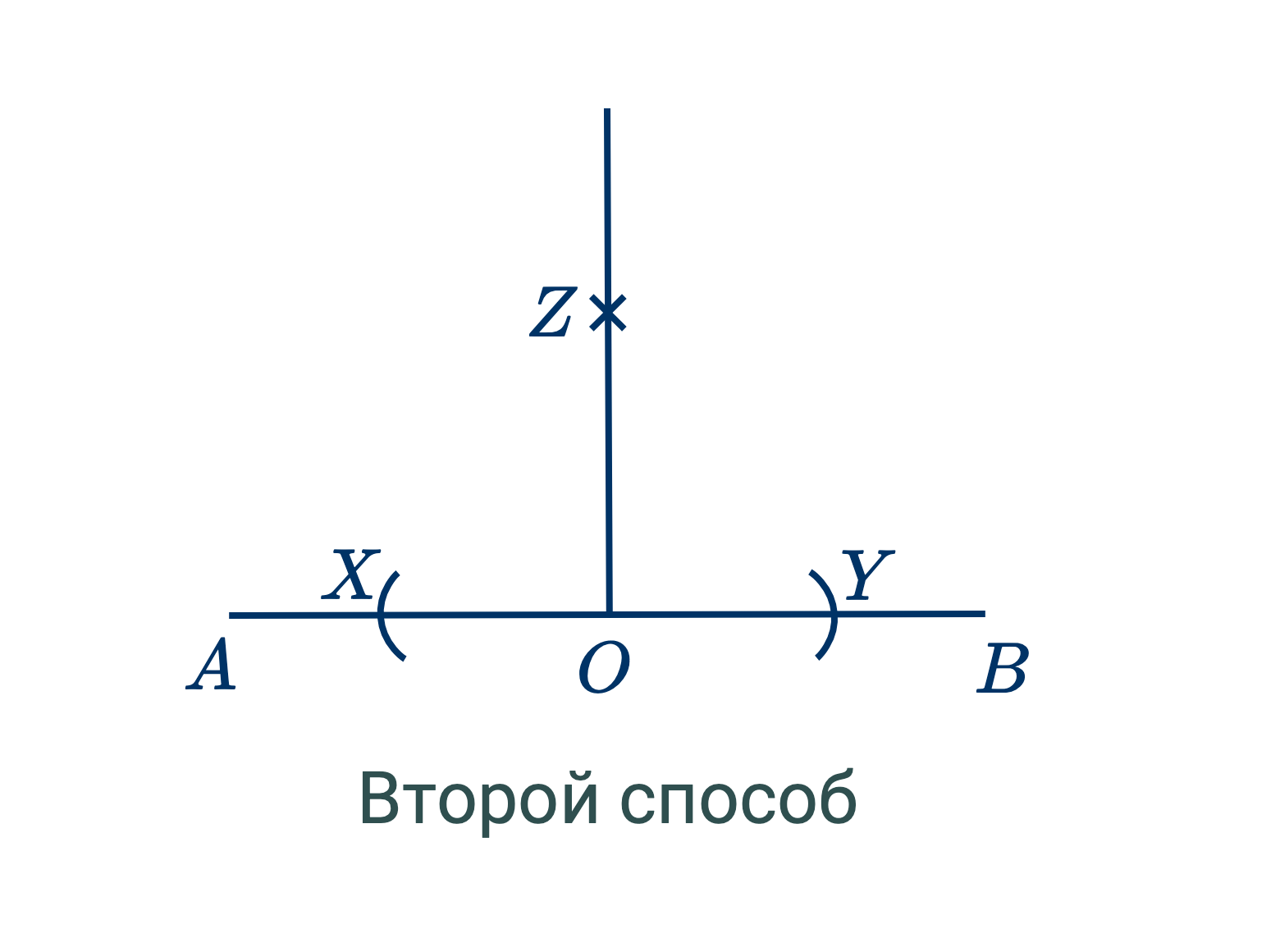
Второй способ (при помощи линейки и циркуля). – Из центра $O$ соответствующим радиусом опишем при помощи циркуля две дуги, пересекающие $AB$ в $X$ и $Y$. Потом из $X$ и $Y$, как из центров, несколько большим радиусом опишем две дуги, пересекающиеся в $Z$. Соединим $Z$ с $O$ при помощи линейки. $ZO$ будет требуемым перпендикуляром. Правильность данного способа будет доказана позже.

Из двух приведенных способов первый короче, но для него требуется, чтобы наугольник действительно имел прямой угол, а мы скопируем его. Второй способ не связан таким условием, хотя для обоих требуется, чтобы края линейки представляли прямую линию, т.е. чтобы кто-нибудь построил такую линейку. Прежде положение прямой линии определяли натягивая веревку; этот способ и теперь практикуется плотниками. Древние египтяне применяли его и даже отмечали прямой угол при помощи веревки.

Теорема.

Два угла, лежащие по одну сторону прямой и образованные другой прямой, исходящей из какой-либо точки первой, равны двум прямым углам.

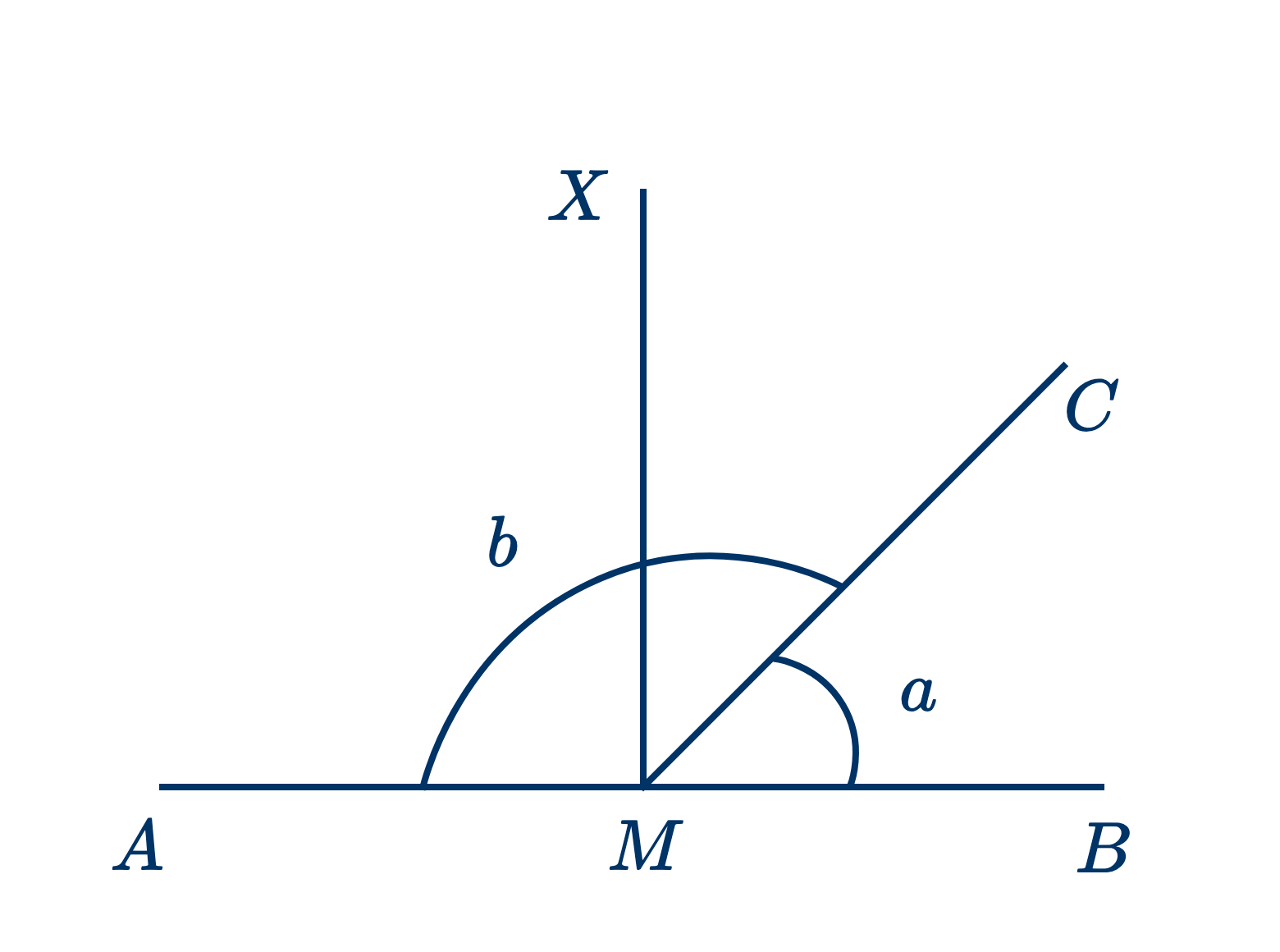
Дано: прямая линия $CM$, встречаясь с прямой $AB$, образует углы $a$ и $b$.
Доказать, что $a+b=2$ прямым углам.

Предположим, что $MX$ есть перпендикуляр к $AB$ (см. теорему .)
Тогда $BMX+XMA=2$ прямым углам.
$BMX$ мы можем заменить равной величиной $a+CMX$ по акс. 11.
Получаем $a+CMX+XMA=2$ прямым углам. $CMX+XMA$ можем заменить углом $b$. Получим $a+b=2$ прямым углам. Q.E.D.

Определение.: Два угла, сумма которых равна прямому, называются дополнительными углами.
Два угла, сумма которых равна двум прямым, называются пополнительными углами.
Два угла, лежащие по одну сторону прямой и образованные другой прямой, исходящей из какой-либо точки первой (как $a$ и $b$), называются смежными углами. Смежные углы – частный случай прилежащих.

Следствие.: Если один из углов, образованных пересечением двух прямых линий, будет прямой, то другой угол также будет прямой. (Фиг.1.)

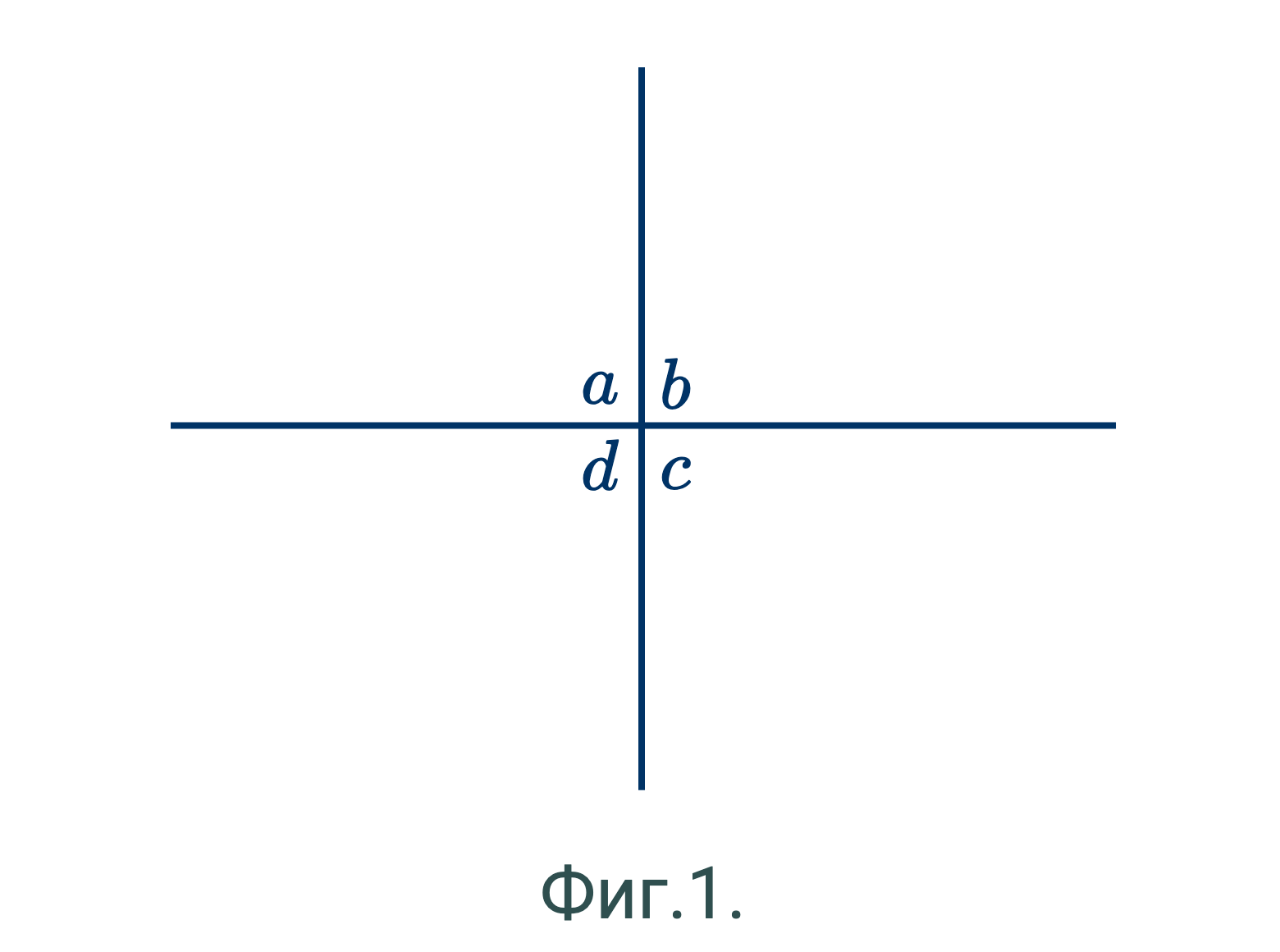
Следствие.: Если одна из двух пересекающихся прямых перпендикулярна к другой, то вторая также перпендикулярна к первой. (Фиг.1.)

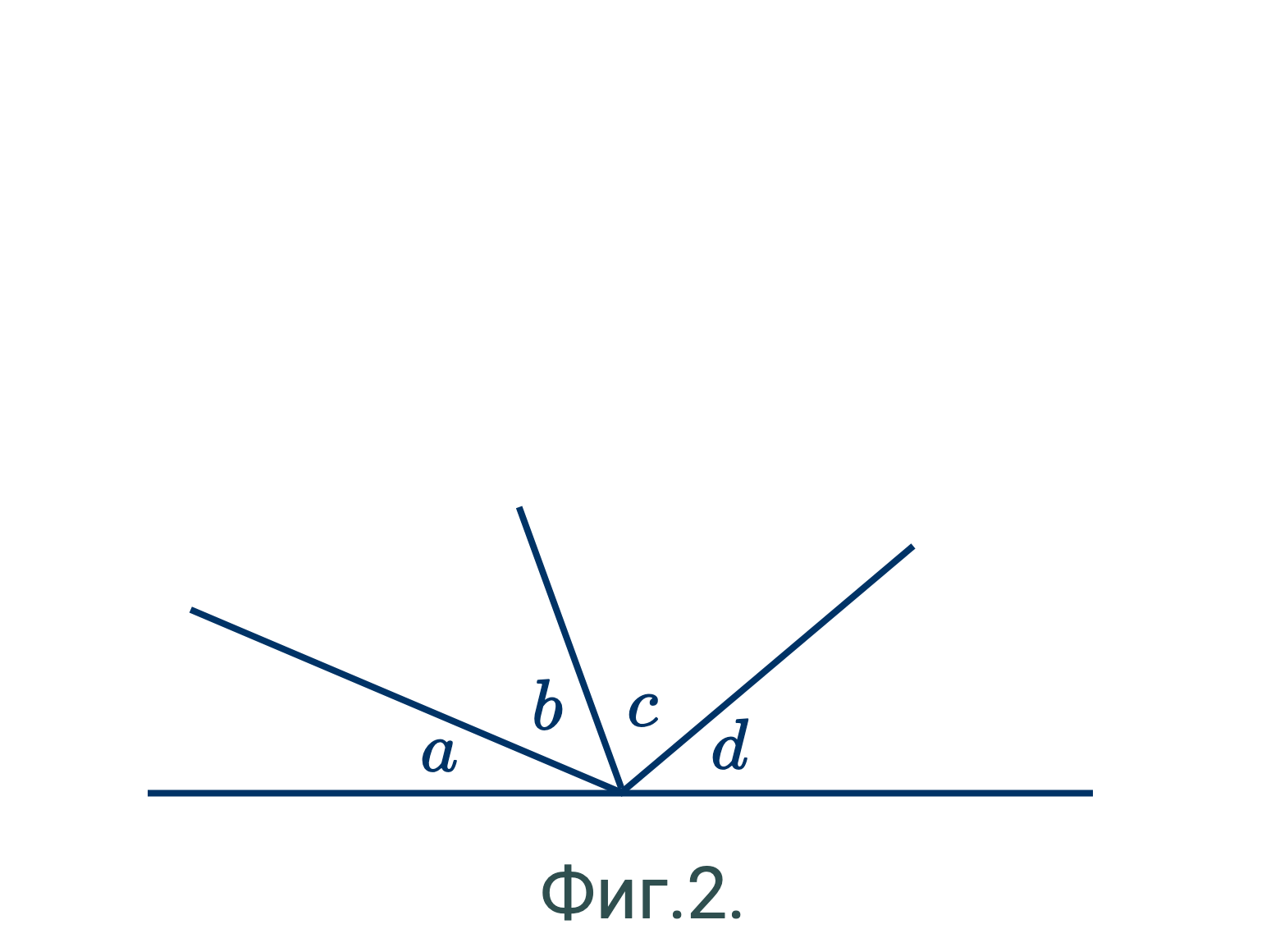
Следствие.: Сумма всех углов, расположенных вокруг точки по одну сторону прямой, равна двум прямым углам. (Фиг.2.)

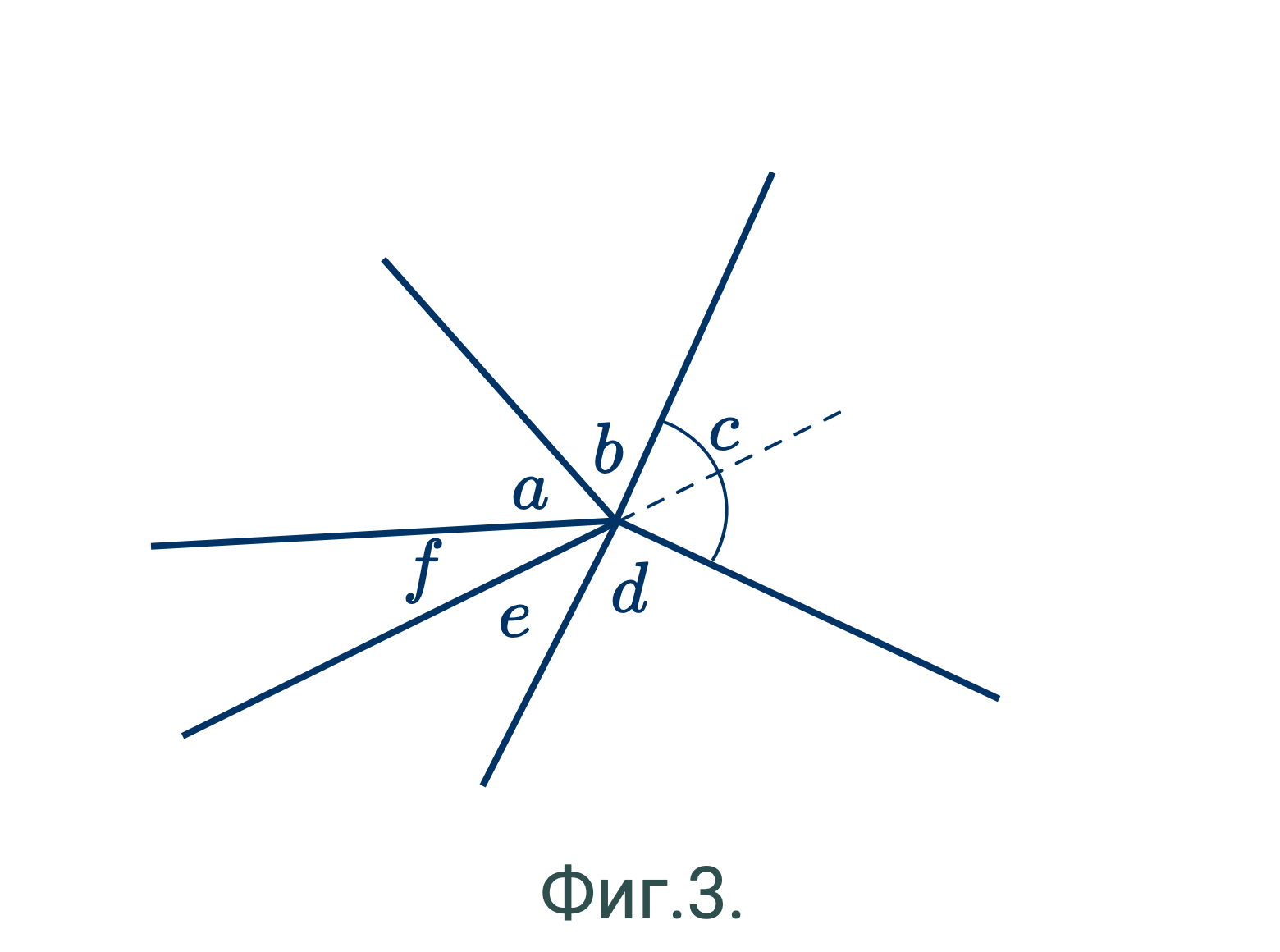
Следствие.: Сумма всех углов, расположенных вокруг точки, равна четырем прямым углам. (Фиг.3.)

Теорема.

Если два прилежащих угла в сумме равны двум прямым углам, то их внешние стороны составляют одну прямую.

Данная теорема является обратною к теореме

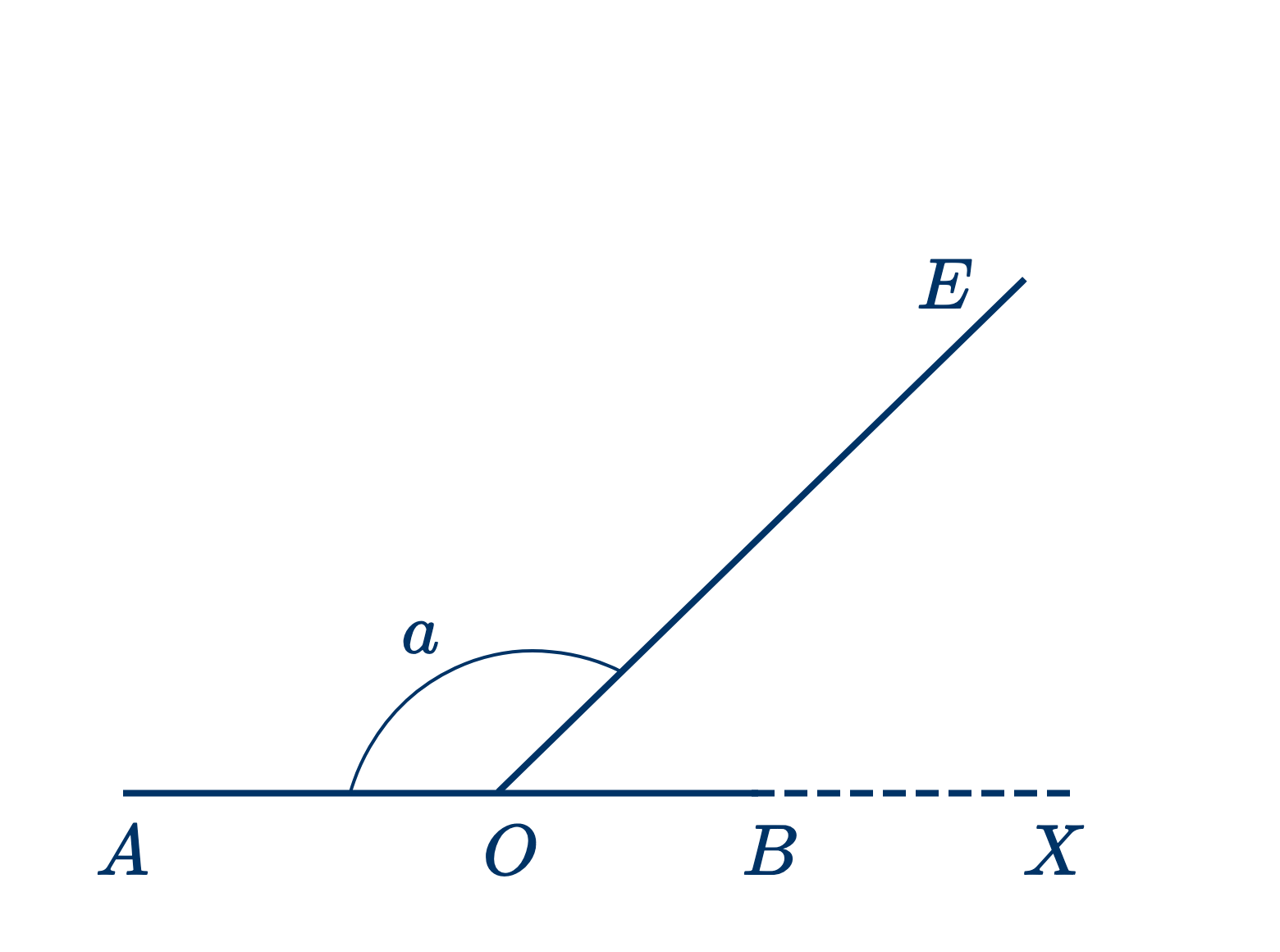
Дано: $a+EOB=2$ прямым углам.
Доказать, что $AO$ и $OB$ образуют одну прямую.

Пусть $OX$ будет продолжение $AO$.
$a+EOB=2$ прямым углам.
$a+EOX=2$ прямым углам (как смежные).
Отсюда $a+EOB=a+EOX$. (см. акс. 1.)
Вычитая $a$ получим, $EOB=EOX$. (см. акс. 3.)
Отсюда $OB$ должно совпасть с $OX$. Иначе один из углов ($EOB$ и $EOX$) включил бы другой, и они не могли бы быть равны. (см. акс. 10.)
Поэтому $OB$ лежит на одной прямой с $OA$. Q.E.D.

Вопрос.: Если два угла смежные и разность между ними равна прямому углу, то чему равен каждый из них?

Вопрос.: По одну сторону прямой расположены три угла. Наибольший из них в три раза, а средний в два раза больше наименьшего. Чему равен каждый угол? Укажите несколько видов их расположения относительно прямой.

Теорема.

Если две прямые пересекаются, то противоположные (или вертикальные) углы равны.

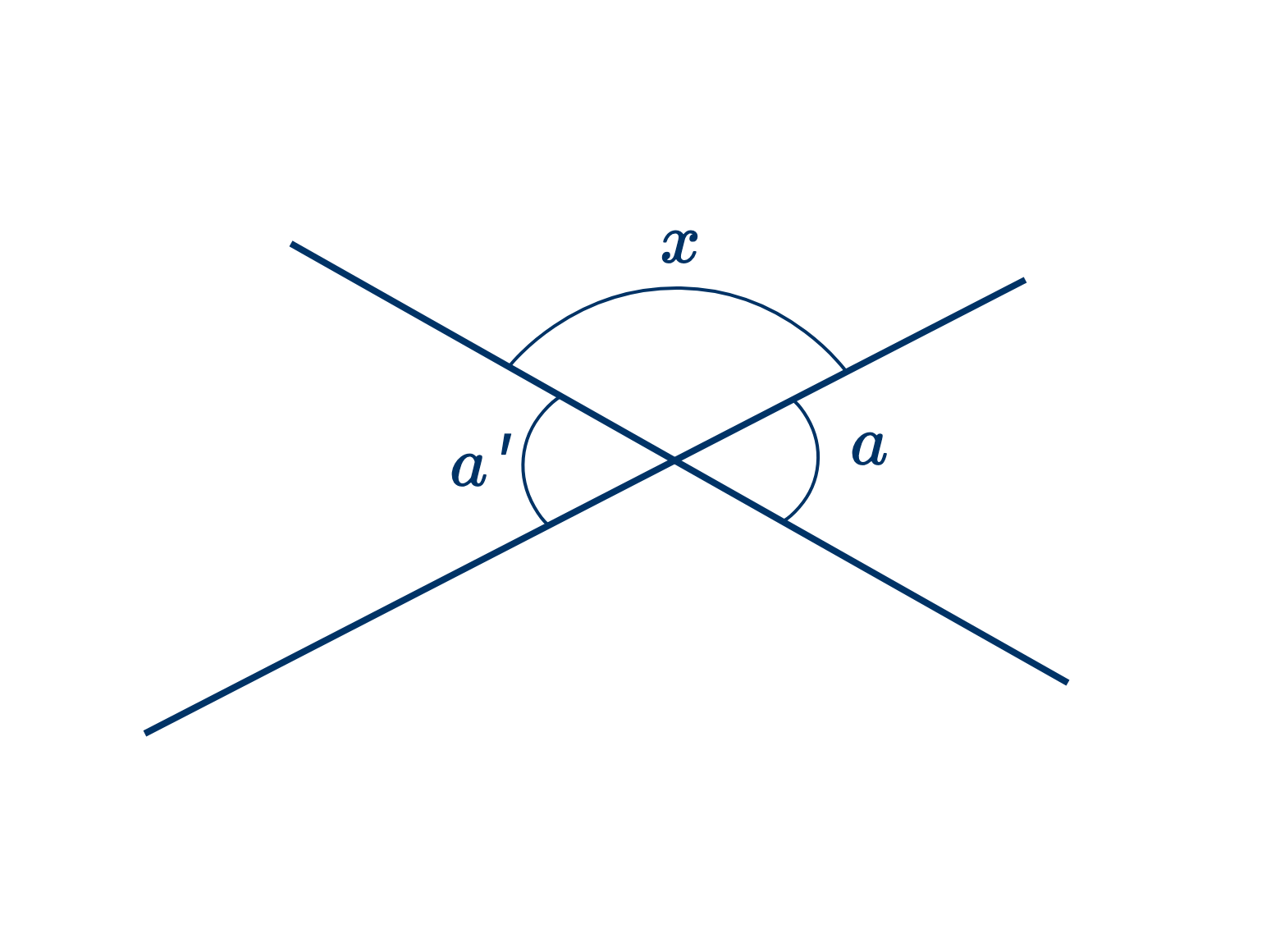
Дано: две пересекающиеся прямые, образующие противоположные углы $a$ и $a'$.
Доказать, что $a=a'$.

$a+x=2$ прямым углам.
$a'+x=2$ прямым углам. (В обоих случаях как смежные.)
Поэтому $a+x=a'+x$ (см. акс. 1.)
Вычитая $x$, получим $a=a'$. (см. акс. 3.) Q.E.D.

← Читать дальше