Параллельные прямые и симметричные фигуры

Определение.: Две прямые, лежащие в одной плоскости и не встречающиеся между собой, сколько бы их ни продолжали, называются параллельными.

Параллельные прямые геометрический чертеж.

Определение.: Две фигуры симметричны по отношению к прямой, называемой осью симметрии, если при вращении около оси они совпадают. (Фиг.1.)

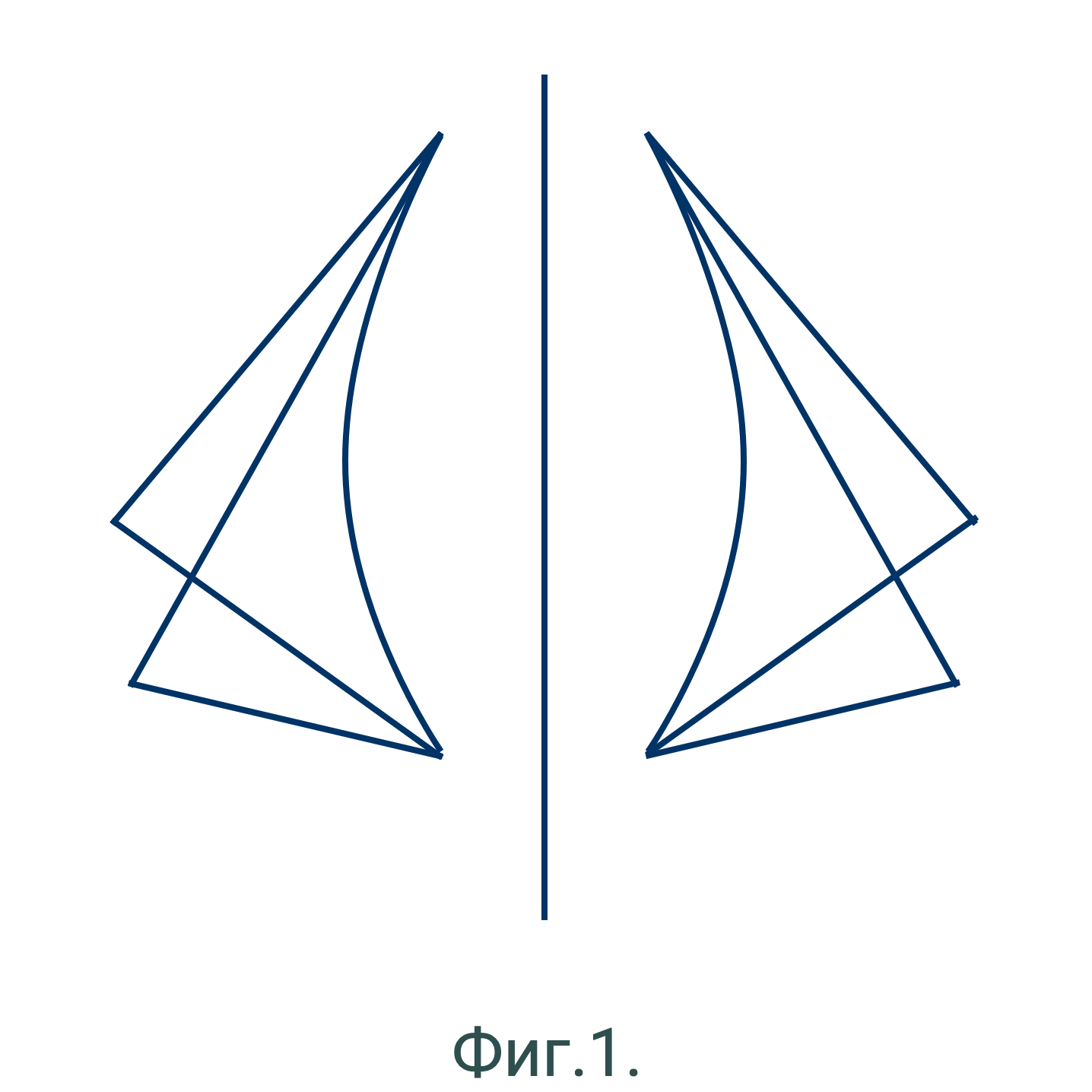
Можно получить ясное представление такого рода симметрии, если нарисовать фигуру чернилами и, прежде чем высохнут чернила, сложить бумагу. Нарисованная и отпечатанная фигуры будут симметричны по отношению к складке, как на (Фиг.2.)

Теорема.

Две прямые, перпендикулярные к третьей, параллельны между собой.

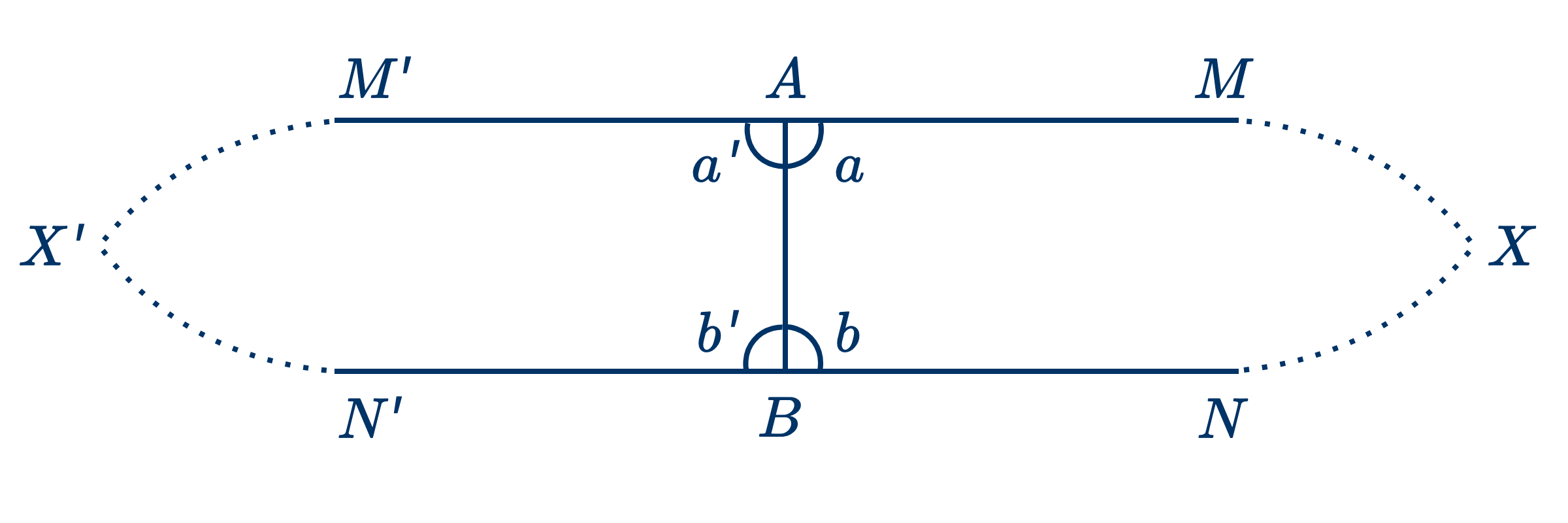
Дано: $AM$ и $BN$ перпендикулярны к $AB$.
Доказать, что $AM$ и $BN$ параллельны.

Если бы $AM$ и $BN$ встретились вправо или влево, положим в $X$, то перегнув фигуру $AXB$ по $AB$, как по оси, мы получили бы симметричное изображение $AX'B$; прямые углы, $a$ и $b$, дали бы соответствующие изображения в $a'$ и $b'$.
Тогда $AM$ и $AM'$ образуют одну и ту же прямую, и $BN$ с $BN'$ также образуют одну и ту же прямую.
(см. теорему .)

Таким образом получилось бы две прямые линии между точками $X$ и $X'$, что невозможно. (см. акс. прямой.)
Поэтому $AM$ и $BN$ не могут встретиться, и так как они лежат в одной плоскости, то должны быть параллельны.
Q.E.D.

Вопрос.: Может ли предыдущая теорема относиться к прямым, не лежащим в одной плоскости?

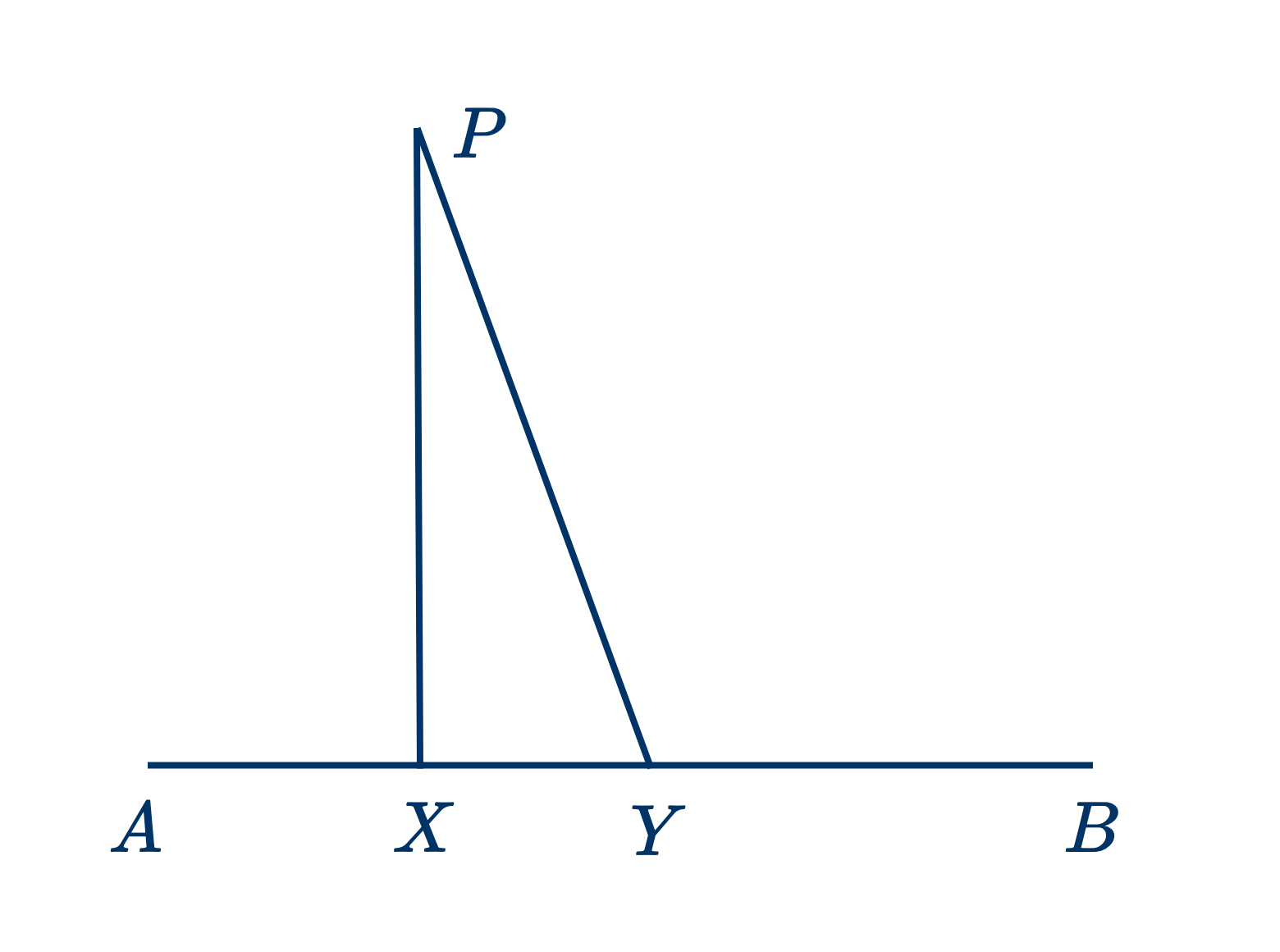
Следствие.: Из данной точки $P$, лежащей вне прямой $AB$, можно опустить на эту прямую один и только один перпендикуляр.

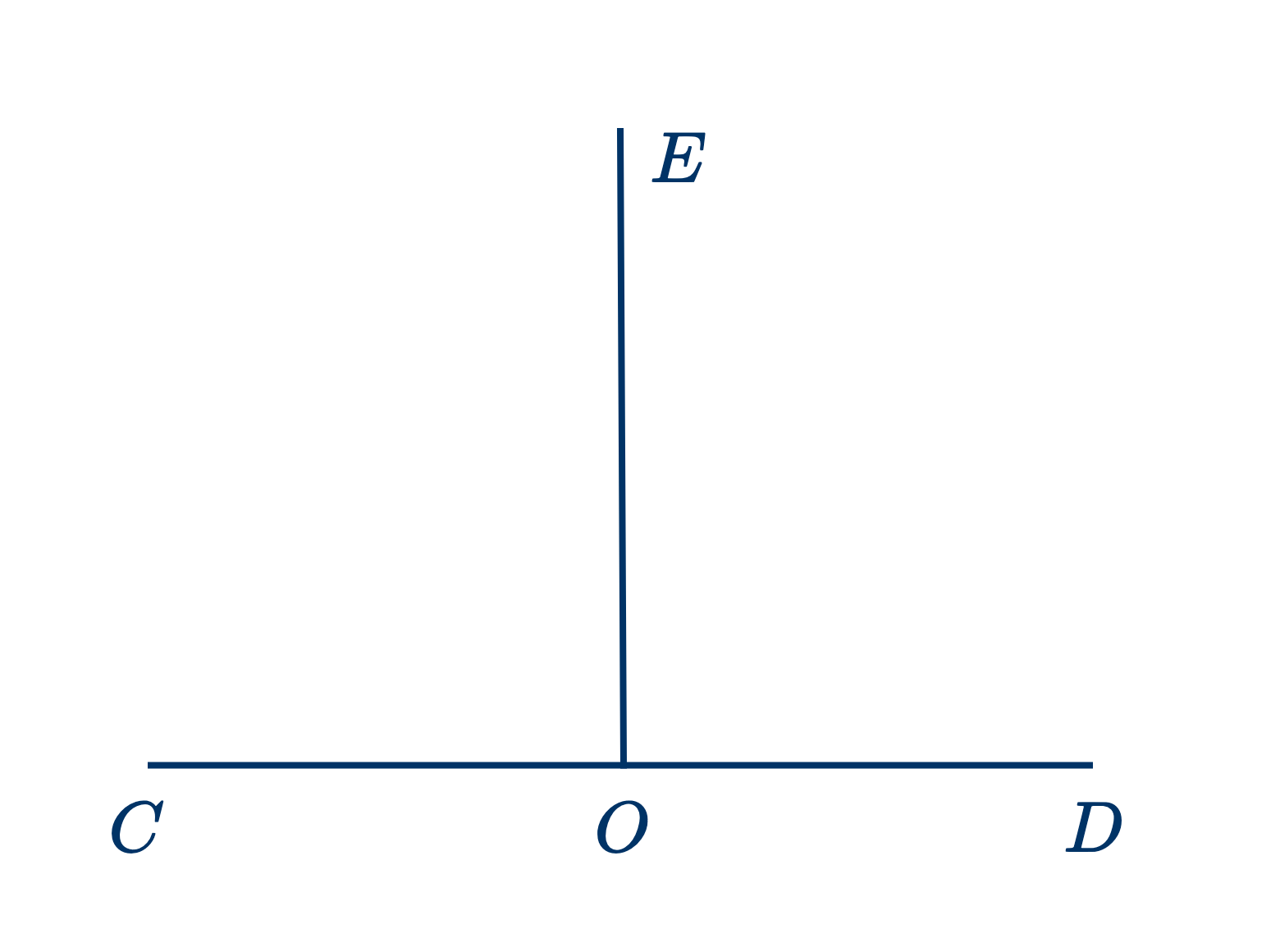
Схема доказательства.: Из точки $O$ на прямой $CD$ проводится перпендикуляр $OE$. (На каком основании это возможно?) $CD$ накладывается на $AB$ и передвигается вдоль ее, пока $OE$ не достигает $P$. (Какая аксиома применяется?)
Во-вторых, предположим, что возможны два перпендикуляра $PX$ и $PY$;
покажите, что это противоречит теореме .

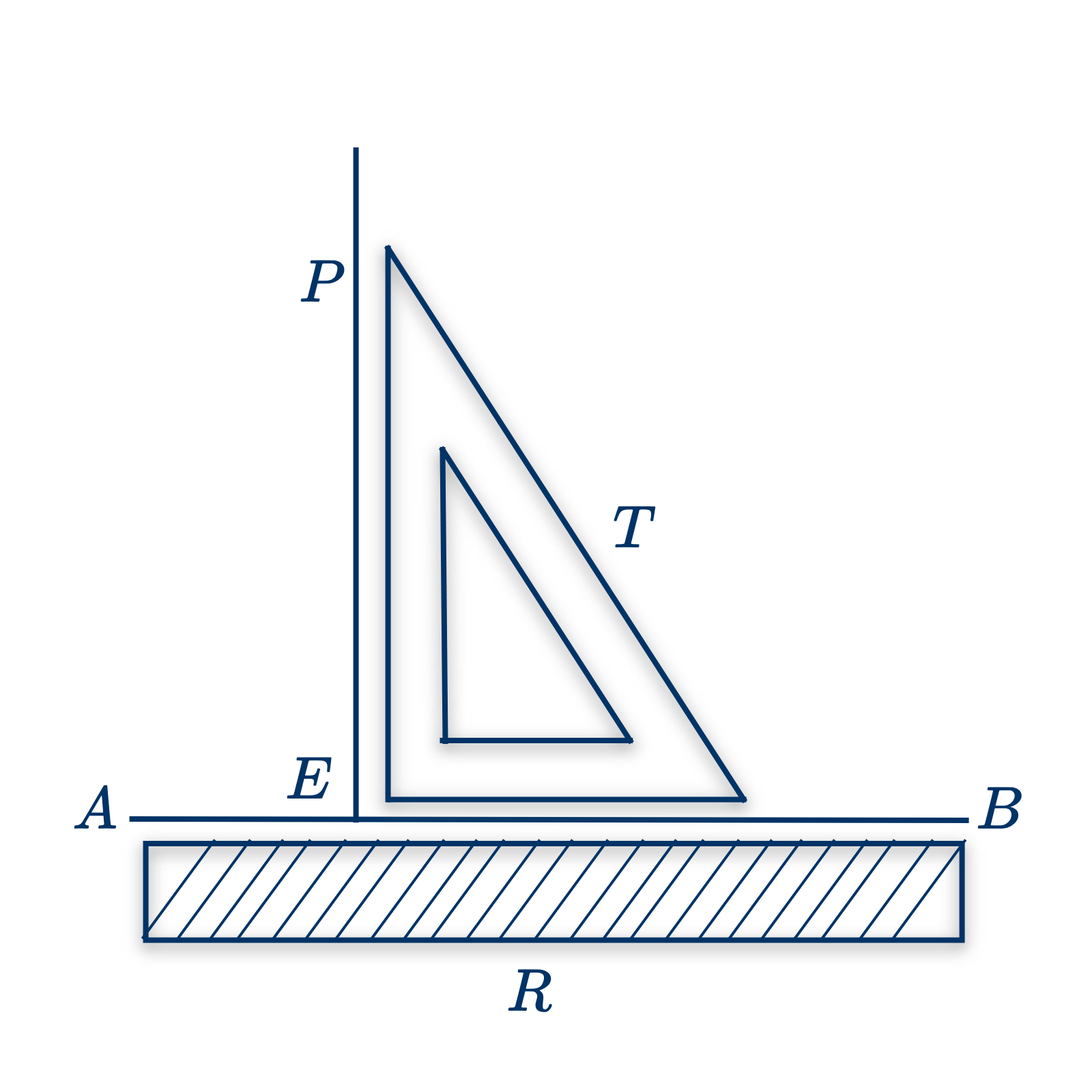
Построение.: Опустить перпендикуляр на прямую $AB$ из точки $P$, лежащей вне прямой.
Первый способ. – Приложим край линейки $R$ к прямой $AB$. Поставим одну сторону прямого угла наугольника $T$ на линейку $R$, а другую поставим перпендикулярно к $AB$. Затем будем передвигать $T$, пока конец перпендикулярной стороны наугольника не совпадет с $P$. Проведем прямую $PE$ вдоль этой стороны. $PE$ будет требуемым перпендикуляром, так как прямая проходит через точку $P$ и перпендикулярна к $AB$.

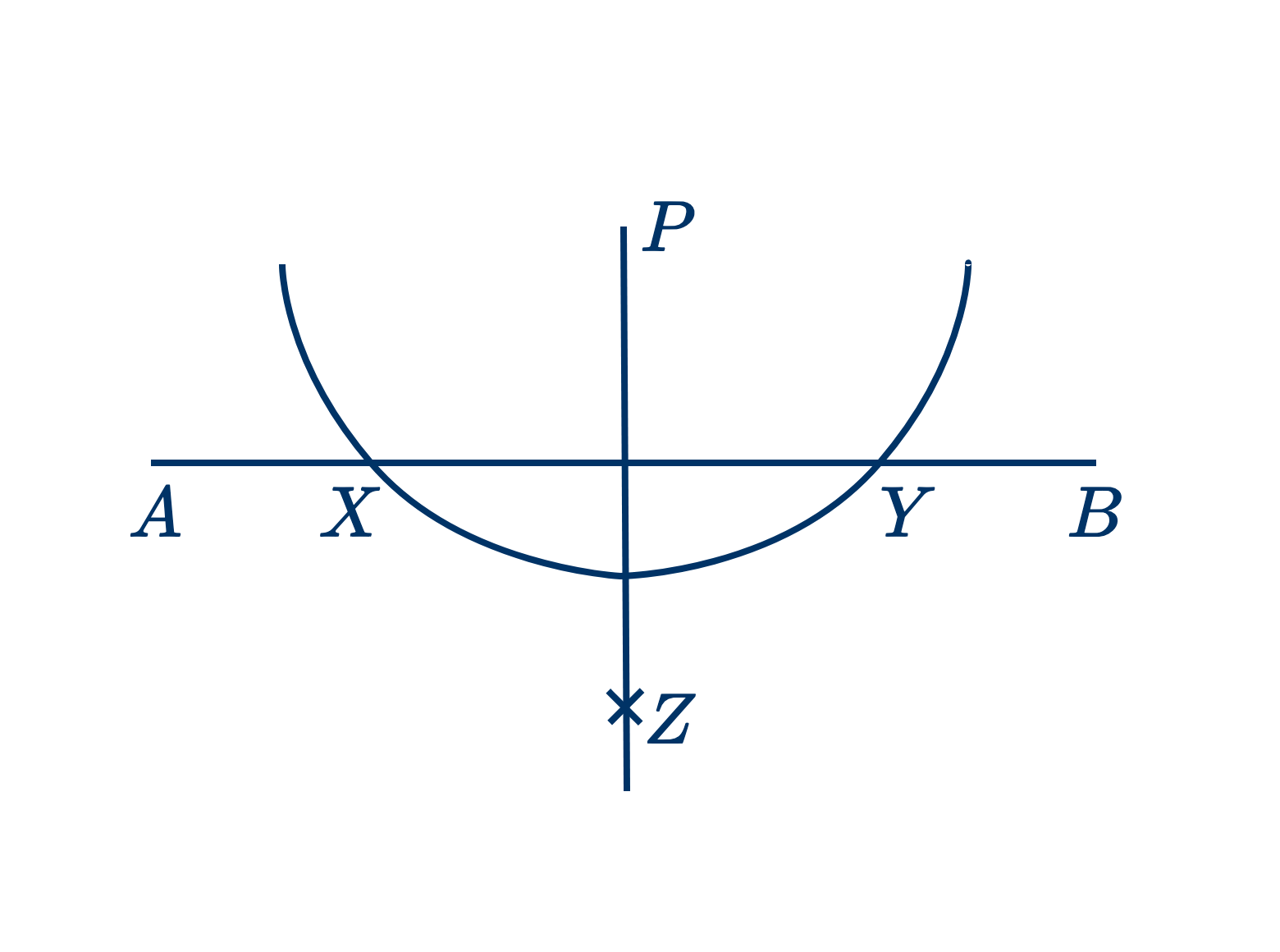
Второй способ. – Из $P$, как из центра, соответствующим радиусом опишем дугу, которая пересечет $AB$ в $X$ и $Y$. Потом из $X$ и $Y$, как из центров, поочередно опишем дуги равными радиусами, пересекающимися в $Z$. Соединим $P$ с $Z$. Это и будет искомый перпендикуляр.
Далее мы обязательно выведем доказательство к этому факту.

Теорема.

Если две прямые параллельны, а третья прямая перпендикулярна к одной из них, то она перпендикулярна и к другой.

Данная теорема является обратною к теореме

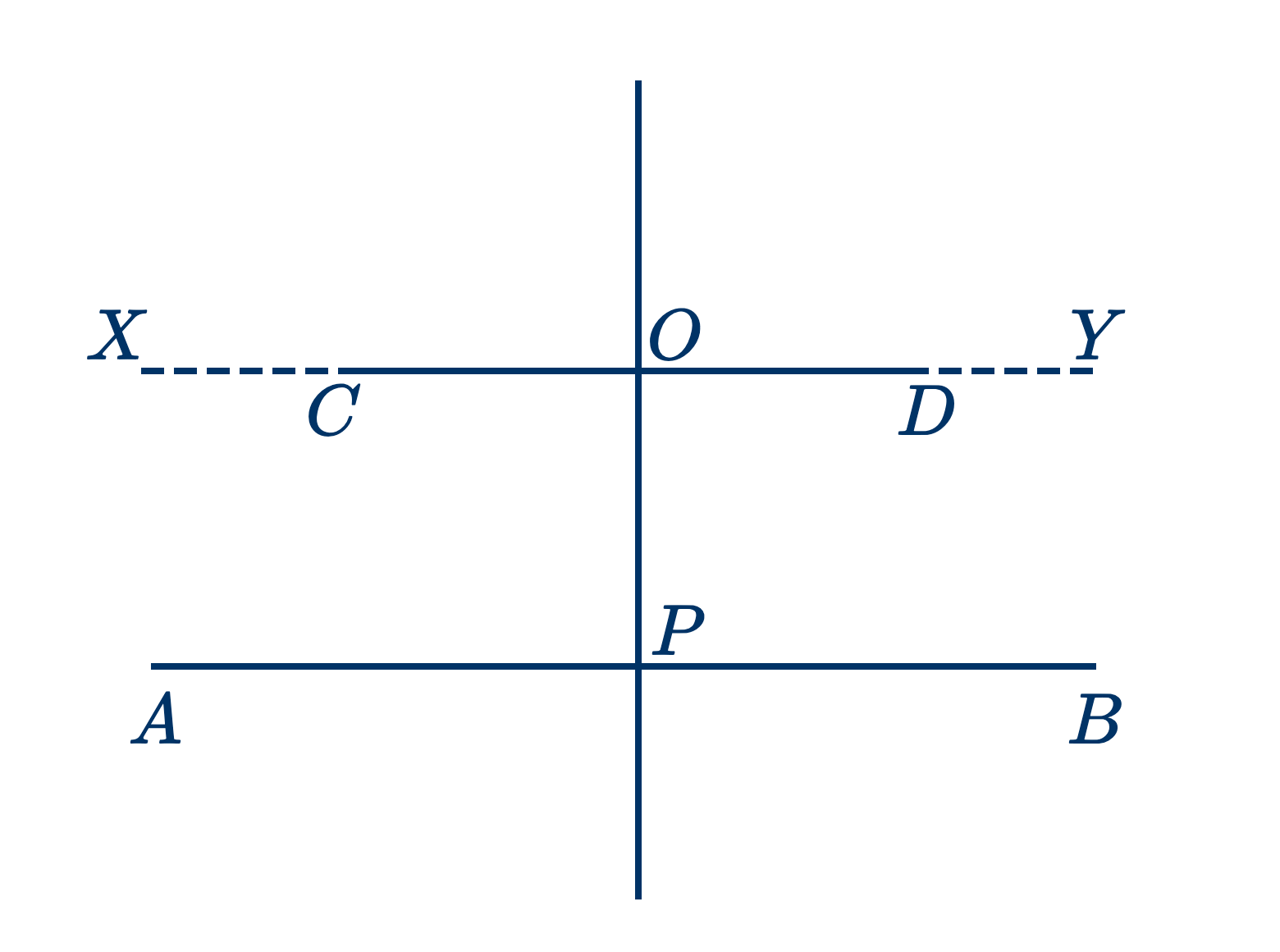
Дано: $CD$ и $AB$ параллельны, $$PO$$ перпендикуляр к $AB$.
Доказать, что $$PO$$ – перпендикуляр к $CD$.

Предположим, что $XY$ проведена через точку $O$ перпендикулярно $OP$.
Тогда $XY$ параллельна $AB$. (см. теорему .)
Но $CD$ параллельна $AB$.
Отсюда $CD$ должна совпасть с $XY$. (см. акс. параллелей.)
Следовательно, $CD$ должна быть перпендикулярна к $$PO$$ , и $OP$ перпендикуляр к $CD$.
Q.E.D.

Построение.: Провести прямую через данную точку $C$ параллельно данной прямой $AB$.
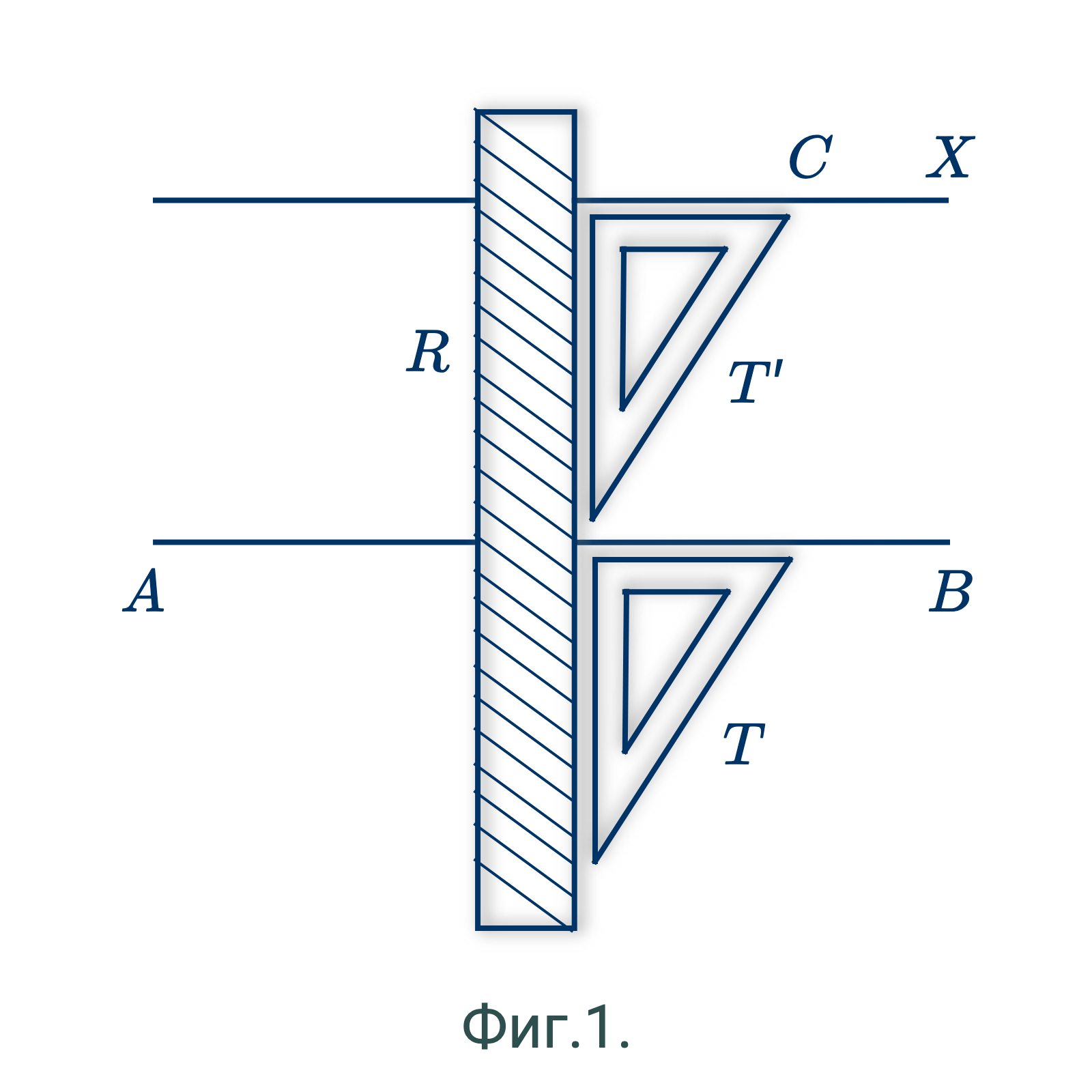
Первый способ. (Фиг.1.) – Поместим наугольник в положение $T$ так, чтобы одна сторона прямого угла совпала с $AB$; затем вдоль другой стороны поставим линейку $R$. Далее прижмем линейку $R$ плотно к бумаге и передвинем $T$ в положение $T'$, пока его край не достигнет $C$. Теперь проведем $CX$. Это и будет искомая параллель. (Почему?)

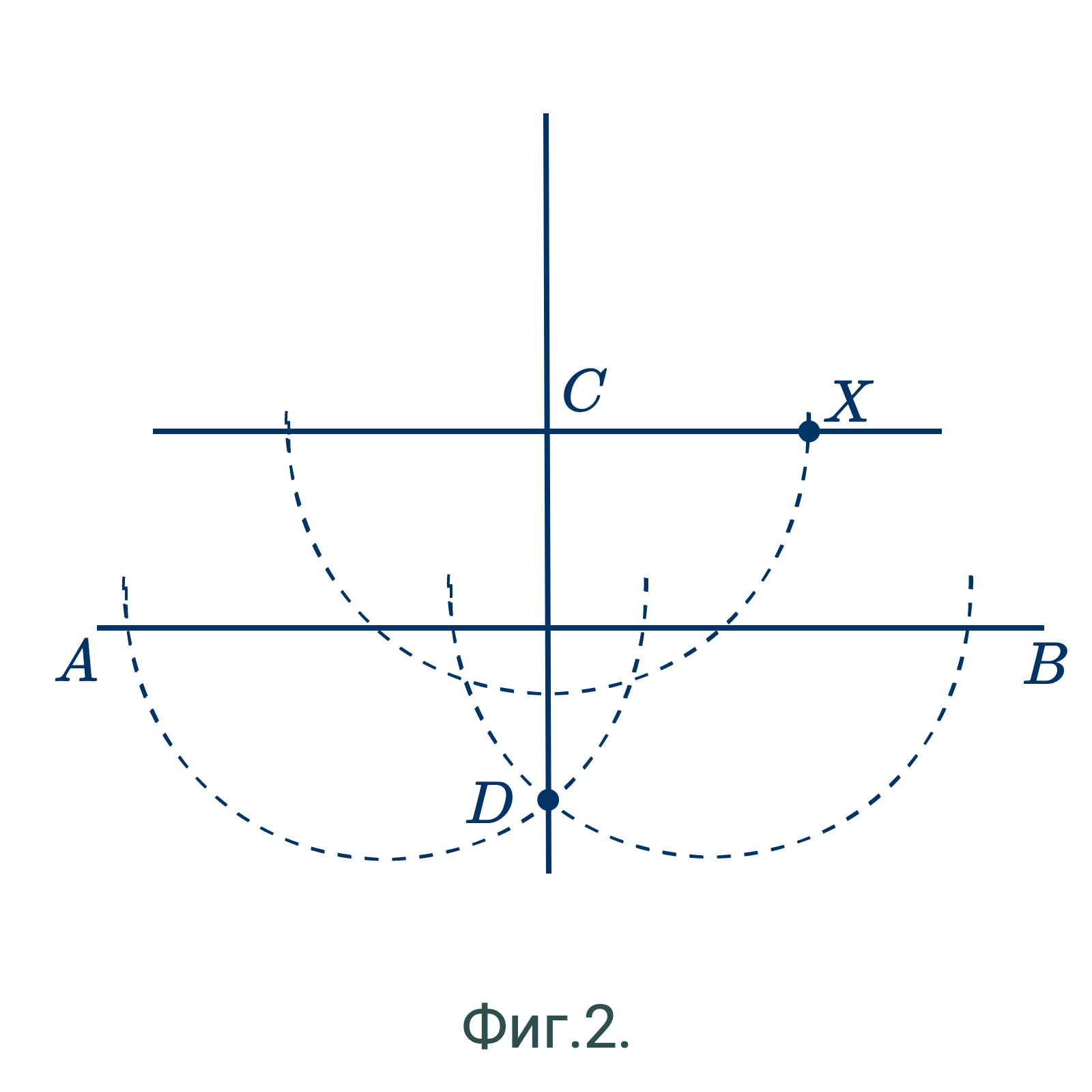
Второй способ. (Фиг.2.) – Из $C$ проведем $CD$ перпендикулярно к $AB$.
Из $C$ проведем $CX$ перпендикулярно к $CD$.
Тогда $CX$ и будет искомая параллель. (Почему?)

Теорема.

Если две прямые параллельны третьей, то они параллельны между собой.

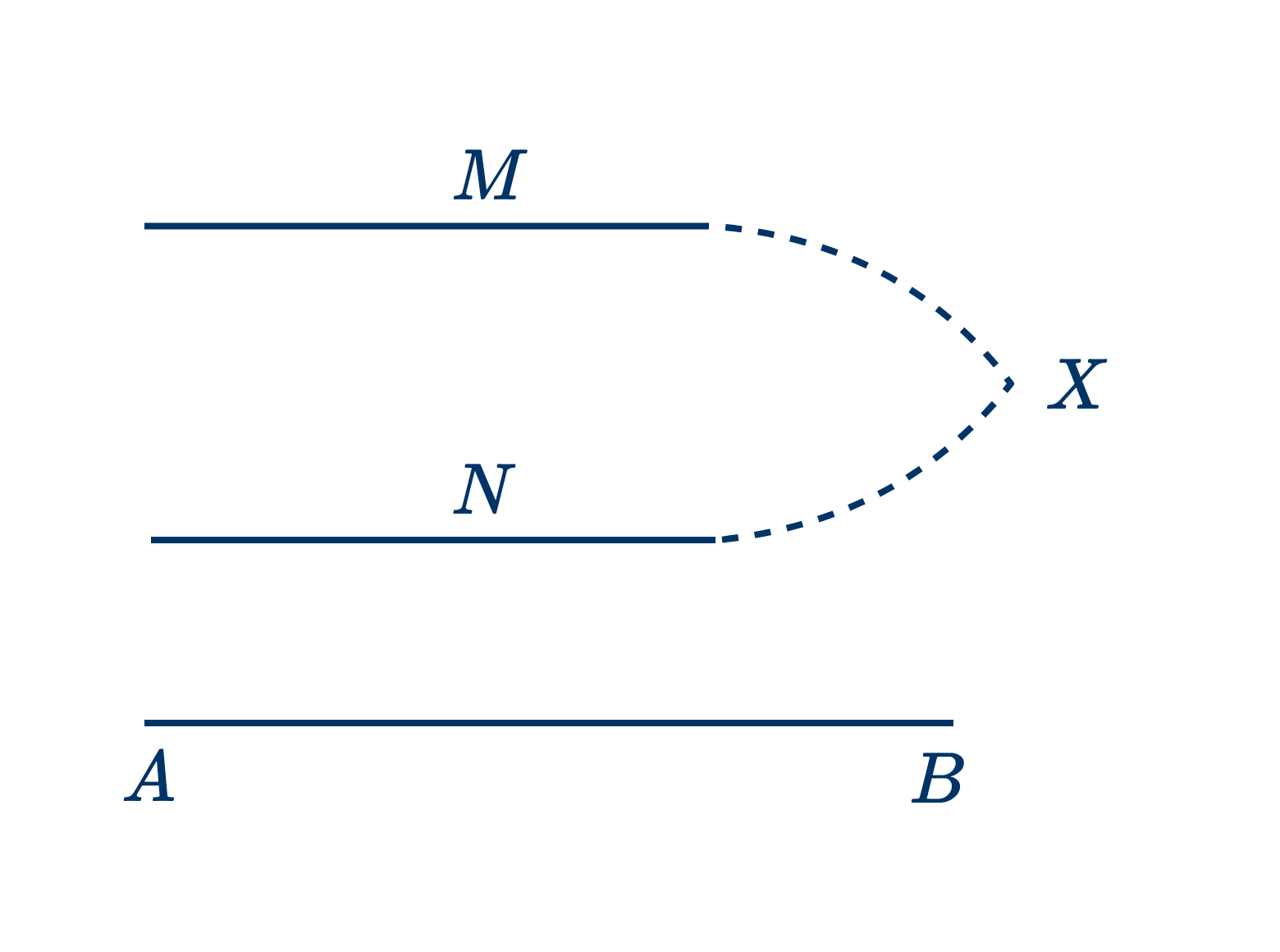
Дано: $M$ и $N$ параллельны $AB$.
Доказать, что $M$ и $N$ параллельны между собой.

Если бы $M$ и $N$ встретились, положим в $X$, то мы бы получили две прямые, параллельные $AB$ и проходящие через одну и ту же точку $X$, что невозможно. (см. акс. параллелей.)
Поэтому $M$ и $N$ не могут встретится и, находясь в одной плоскости, должны быть параллельны.
Q.E.D.

Определение.: Когда две прямые пересекаются третьей, то образуются следующие $8$ углов:
$a, \ b, \ a', \ b',$ внутренние углы.
$A, \ B, \ A', B',$ внешние углы.
$a$ и $a'$ или $b$ и $b'$, накрест-лежащие внутренние углы.
$A$ и $A'$ или $B$ и $B'$, накрест-лежащие внешние углы.
$A$ и $a', \ b$ и $B', \ B$ и $b'$ или $a$ и $A',$ соответственные углы.

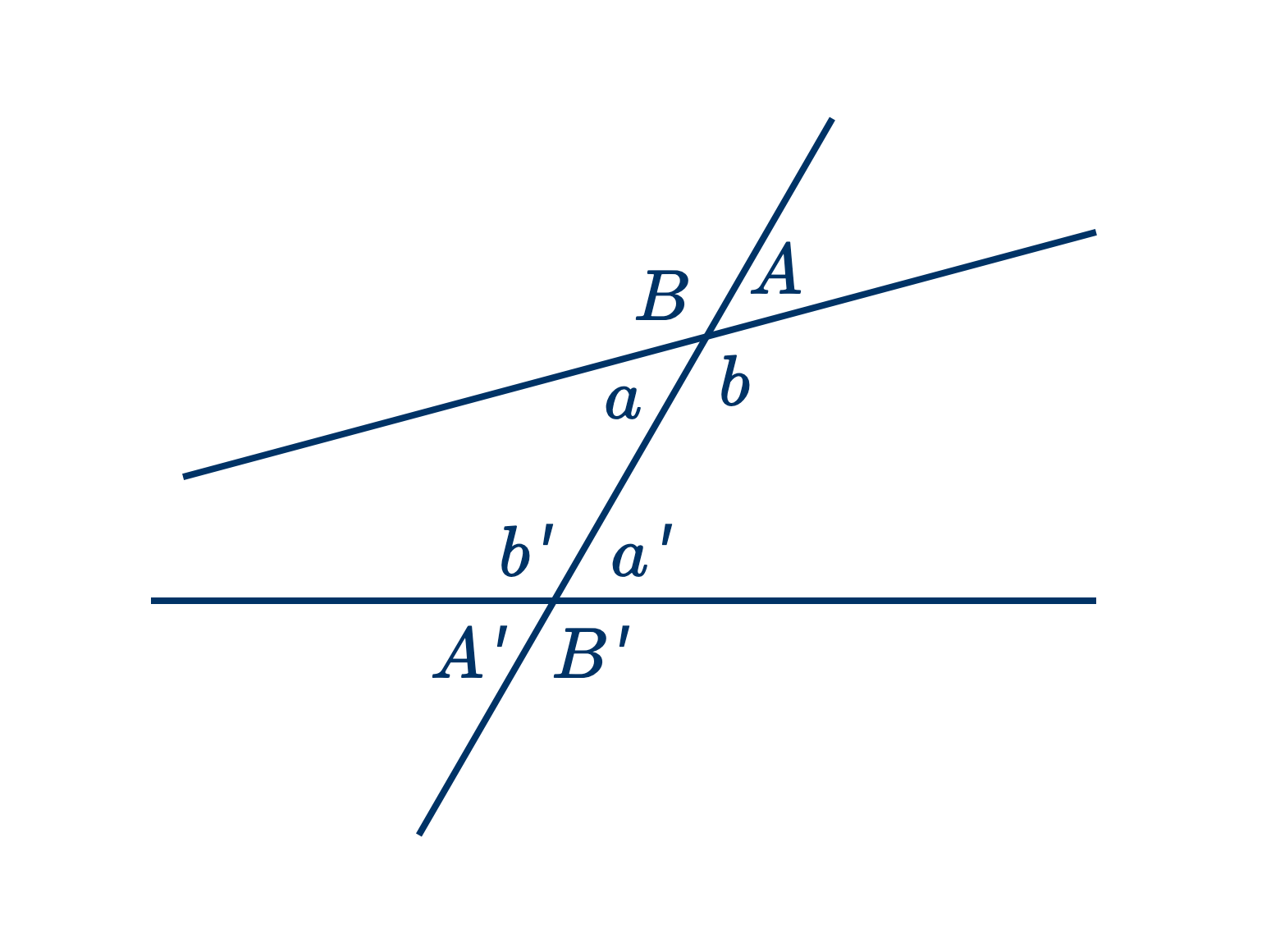
Углы при пересечение двух прямых третьей прямой.

Вопросы.: Которые из восьми углов всегда равны и почему?
Если $A=A',$ то какие еще углы также равны $A$ и почему?
Все ли остальные углы равны, и если равны, то почему?
Если $A=A',$ также $A=B,$ то какие еще углы равны и почему?

Определение.: Две фигуры симметричны относительно точки, называемой центром симметрии, если одна из них, вращаясь около этой точки и сделав полукруг, совпадает с другой.
Одна фигура называется симметричной относительно точки, называемой центром симметрии, если при вращении вокруг этой точки каждая часть фигуры, сделав полукруг, займет место, прежде занимаемое другой частью.

Две фигуры симметричные относительно точки.

Одна фигура симметричная относительно точки.

Теорема.

Если при пересечении двух прямых какой-нибудь третьей прямой окажется, что сумма внутренних односторонних углов равна двум прямым, то первые две прямые параллельны.

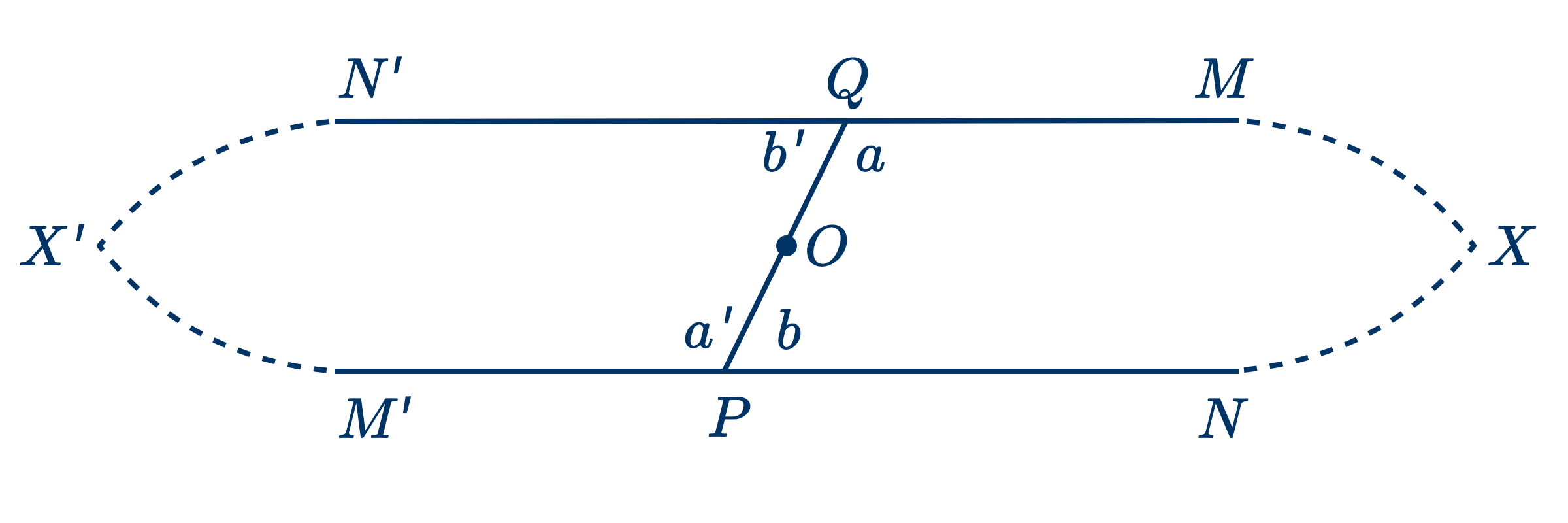
Дано: $$PQ$$ пересекает $QM$ и $PN$ так, что $a$ и $b$ расположены по одну сторону $$PQ$$ и в сумме равны двум прямым углам.
Доказать, что: $QM$ и $PN$ параллельны.

Повернем фигуру $QMXNP$ вокруг $O$, середины $$PQ$$ , на полоборота: она займет симметричное положение $PM'X'N'Q$, а $P$ и $Q$ поменяются местами.
Угол $a$ является пополнительным для угла $b$.
Отсюда, если $a$ примет положение $a'$, $PM'$ должна быть продолжением $PN$ (см. теорему .)
Точно также $QN'$ есть продолжение $QM$.
Теперь, если бы эти прямые встретились справа от $$PQ$$ , например, в точке $X$, то они должны были бы встретиться и слева, в точке $X'$.
В результате получились бы две прямые между двумя точками, $X$ и $X'$, что невозможно. (см. акс. прямой.)
Если они не встретятся справа от $$PQ$$ , они также не могут встретиться и слева от нее.
Отсюда следует, что $QM$ и $PN$ не встречаются; а так как они находятся в одной плоскости, то они параллельны.
Q.E.D.

Замечание.: Нужно заметить, что предыдущие теоремы основаны на двух из трех геометрических аксиом, помещенных в §2, а именно: на аксиоме наложения, допускающей вращение фигуры вокруг $O$ без изменения и аксиоме прямых, приведенной для доказательства того, что не может быть двух прямых между $X$ и $X'$. Аксиома параллелей (через данную точку можно провести только одну прямую, параллельную данной прямой) приводилась только для теорем и . Математики старались освободиться от нее, но безуспешно. Действительно, Лобачевский в 1829 г. доказал, что мы никогда не освободимся от аксиомы о параллелях, если не признаем, что пространство, в котором мы живем, совершенно отлично от того, каким мы его себе представляем по опыту. Лобачевский старался представить другой вид вселенной, в которой аксиома параллелей оказалась бы неверной. Этот воображаемый вид пространства называется Неевклидовым, тогда как пространство, в котором мы живем, называется Евклидовым, потому что Евклид первый написал систематическую геометрию пространства. В пространстве Лобачевского теорема будет верной, но теоремы и не верными.

Построение.: Разделить данный отрезок $AB$ пополам.

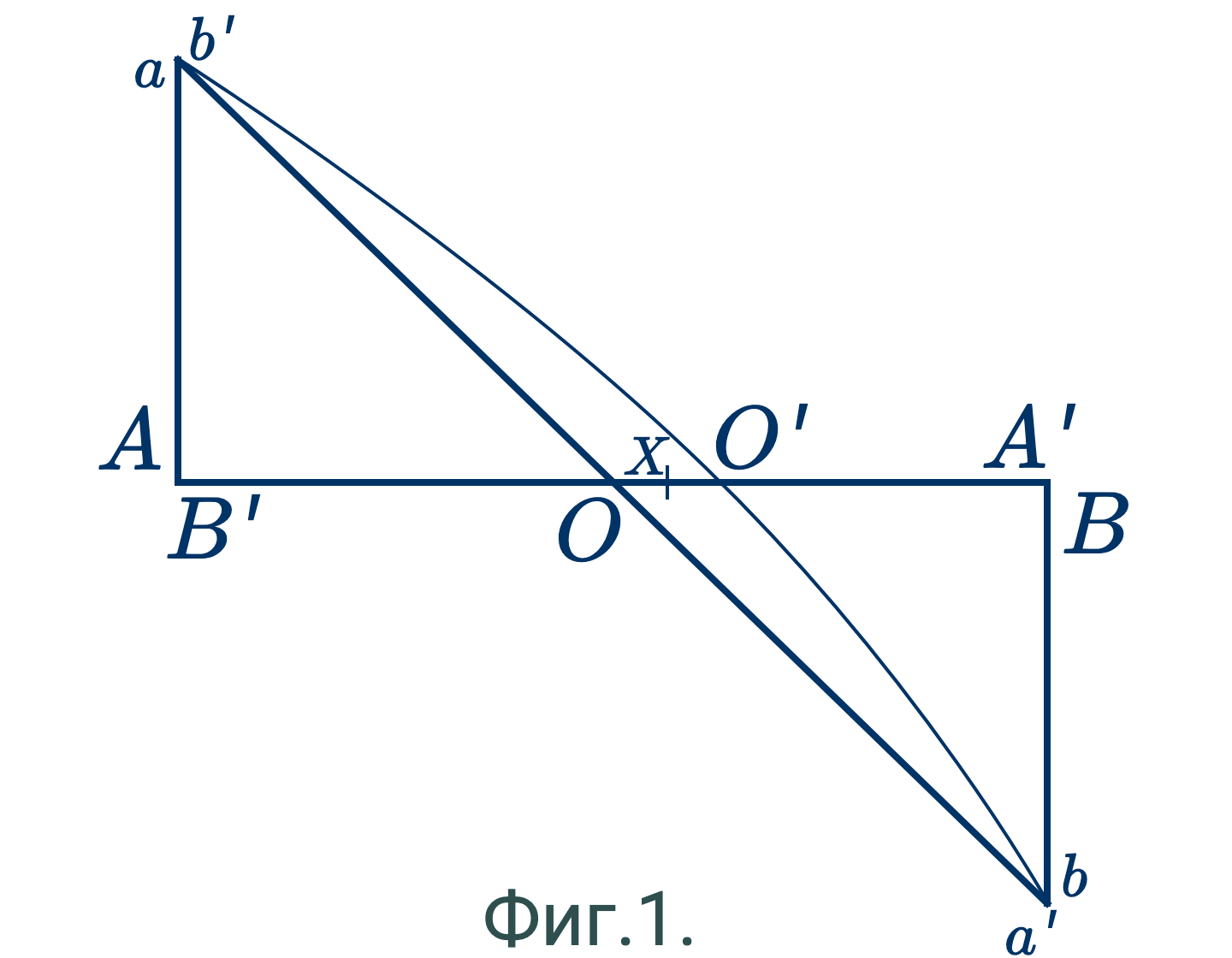
Доказательство. – Положим, что средняя точка $AB$ будет не $O$, а какая-нибудь другая точка $X$.
Повернем всю фигуру вокруг $X$, пока отрезок $AX$ не совпадет с равным ему отрезком $BX$, $A$ упадет в $B$ (назовем это положение $A$ через $A'$) и $B$ в $A$ (назовем это положение $B$ через $B'$). $O$ займет положение $O'$ по другую сторону от $X$.
Тогда перпендикуляр $Aa$ пойдет вдоль $Bb$. (см. теорему .)
И $a$ упадет в $b$ (назовем это положение $a$ через $a'$).
И таким же образом $b$ упадет в $a$ (назовем это положение $b$ через $b'$).
Тогда прямая $aOb$ займет положение $a'O'b'$.
То-есть, через две точки $a$ и $b$ будут проведены две прямые, что невозможно. (см. акс. прямой.)
Итак, предположение, что $O$ не есть средняя точка, неверно, следовательно, $O$ есть средняя точка.
Q.E.D.

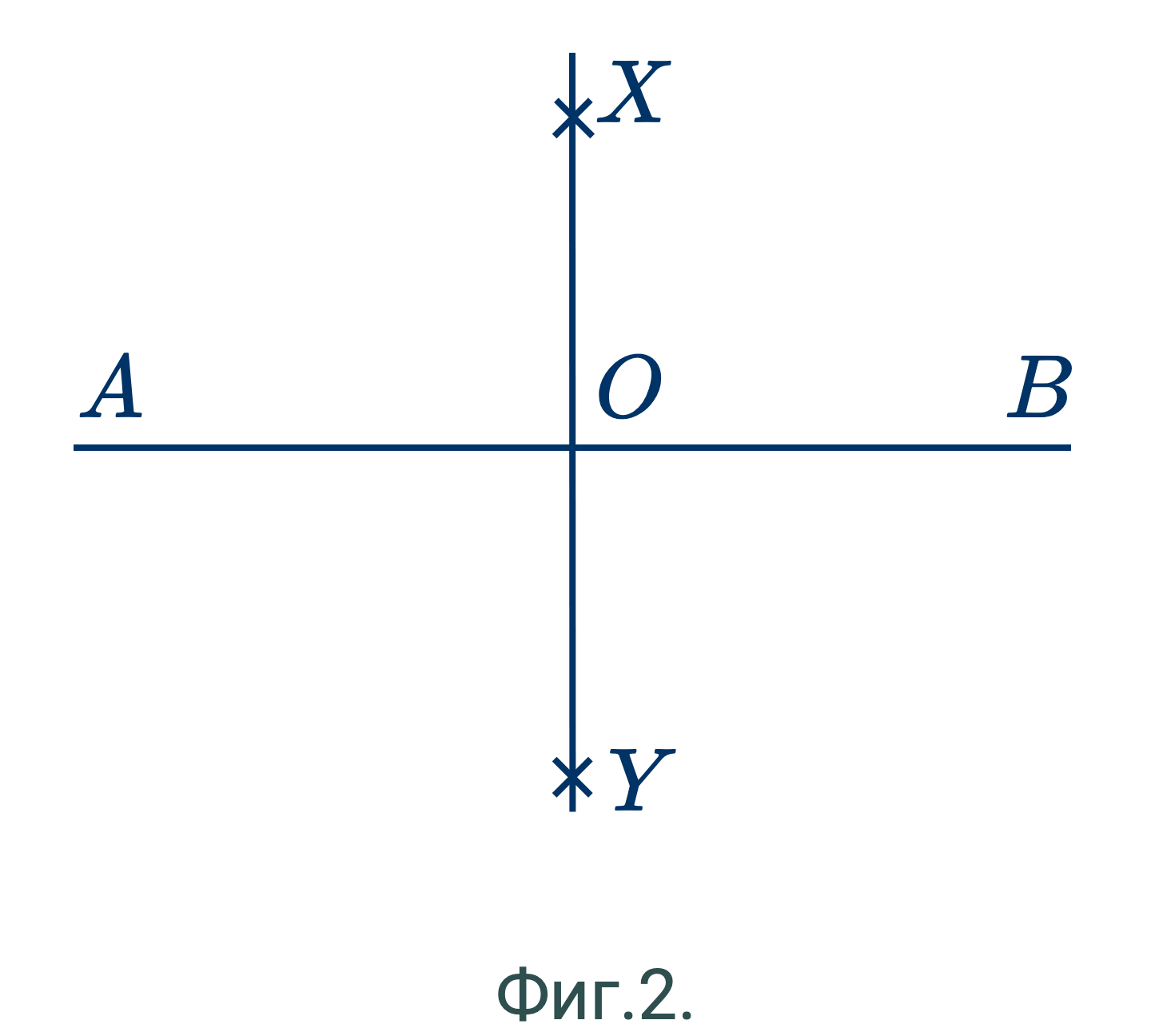
Второй способ. (Фиг.2.) – Из $A$ и $B$, как центров, одинаковым радиусом опишем дуги; они пересекутся в $X$ и $Y$. Соединим $X$ с $Y$; прямая $XY$ пересечет $AB$ в точке $O$; это и будет искомая средняя точка. Этот способ можно будет доказать позже.

Теорема.

Если при пересечении двух прямых какой-нибудь третьей прямой окажется, что внутренние накрест-лежащие углы равны, то первые две прямые будут параллельными.

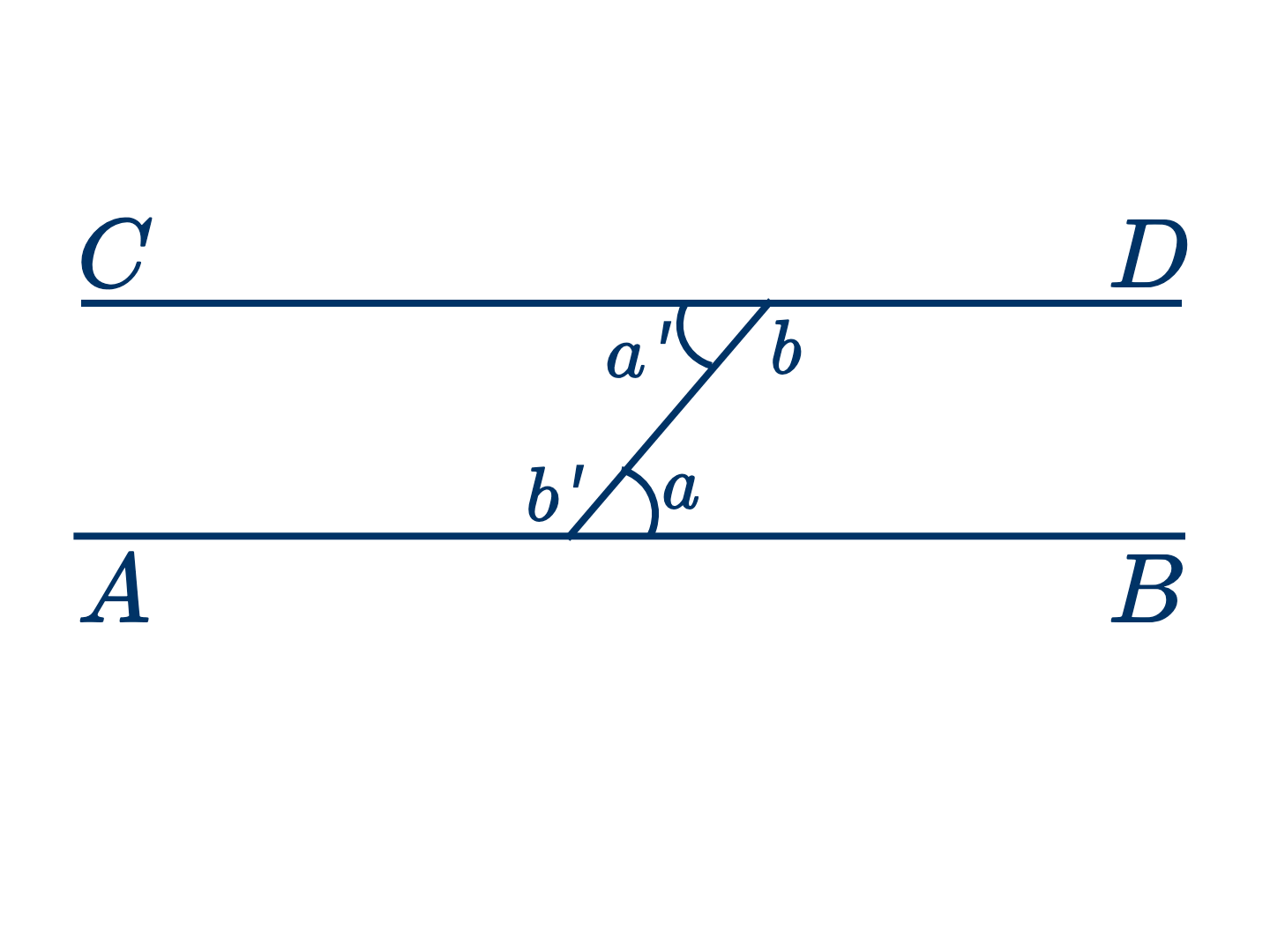
Дано: $a=a'$.
Доказать, что $AB$ и $CD$ параллельны.

$a'+b=2$ прямым углам (как смежные).
Заменим $a'$ равным ему $a$.
Тогда $a+b=2$ прямым углам.
Поэтому $AB$ параллельна $CD$. (см. теорему .)
Q.E.D.

Следствие.: Если при пересечении двух или более прямых третьей соответственные углы равны, то эти прямые параллельны.

Следствие.: Если при пересечении двух прямых третьей внешние накрест-лежащие углы равны, то эти прямые параллельны.

Указание.: Сведите утверждения к теореме с помощью теоремы .

Теорема.

Если две параллельные прямые пересечены третьей, то сумма двух внутренних односторонних углов равна двум прямым углам.

Данная теорема является обратною к теореме

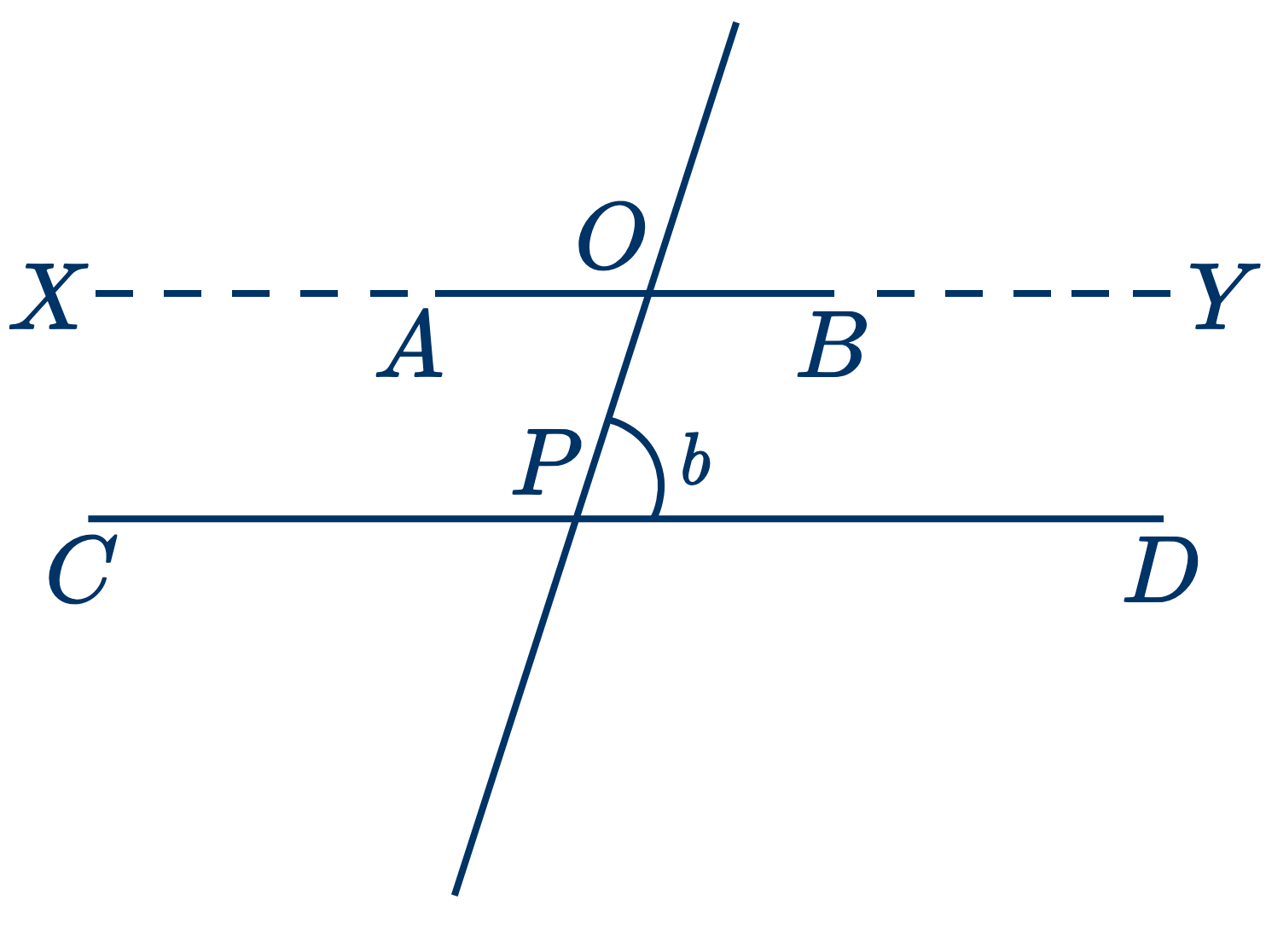
Дано: $AB$ и $CD$ параллельны и пересечены прямой $OP$.
Доказать, что $b+BOP=2$ прямым углам.

Предположим, что $XY$ прямая, проведенная через $O$ так, что $b+YOP=2$ прямым углам.
Тогда $XY$ параллельна $CD$. (см. теорему .)
Но $AB$ параллельна $CD$ по условию.
Отсюда $AB$ совпадет с $XY$. (см. акс. параллелей.)
Далее $BOP=YOP$.
Отсюда $b+BOP=b+YOP$. (см. акс. 2.)
Но $b+YOP=2$ прямым углам по построению.
Поэтому $b+BOP=2$ прямым углам. (см. акс. 1.)
Q.E.D.

Теорема.

Если две параллельные прямые пересечены третьей прямой, то внутренние накрест-лежащие углы равны.

Данная теорема является обратною к теореме

Дано: $AB$ и $CD$ параллельны.
Доказать, что $b=AOP$.

Положим, что $XY$ прямая, проведенная через точку $O$ так, что $XOP=b$.
Тогда $XY$ параллельна $CD$. (см. теорему .)
Но $AB$ параллельна $CD$ по условию.
Отсюда $AB$ совпадет с $XY$. (см. акс. параллелей.)
И $AOP=XOP$.
Но $b=XOP$ по построению.
Поэтому $AOP=b$. (см. акс. 1.)
Q.E.D.

Следствие.: Если две или более параллели пересечены прямой, то соответственные углы равны.

Указание.: Сведите к теореме .

Замечание.: Из предыдущих теорем и следствий вытекает, что если две параллельные пересекаются третьей прямой, как на фигуре, то:

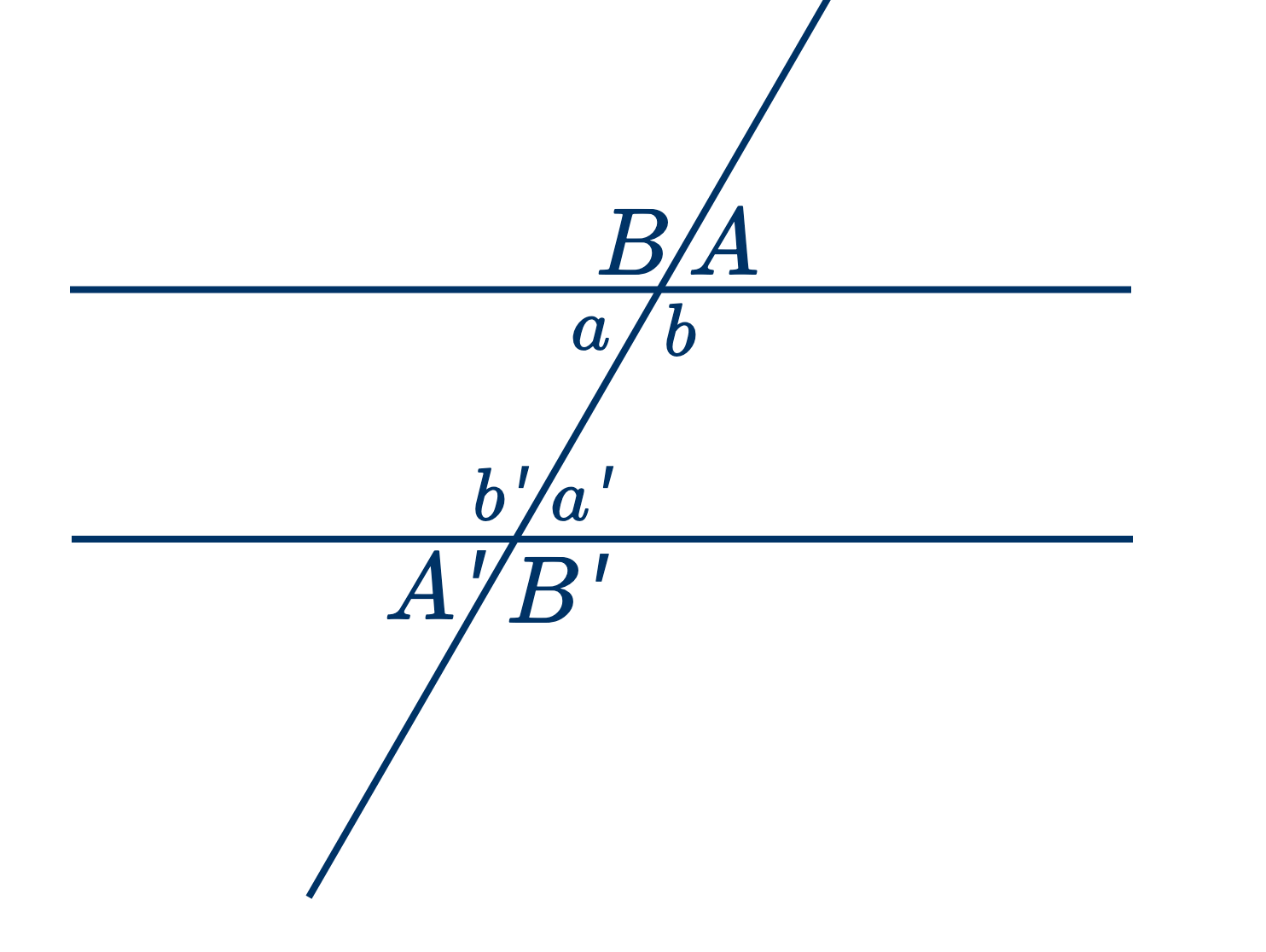
$$A=a=a'=A',$$ $$B=b=b'=B'.$$ И каждый угол первого ряда является пополнительным для каждого угла второго ряда.

Теорема.

Если стороны одного угла соответственно параллельны сторонам другого угла, то такие углы или равны, или в сумме составляют два прямых (пополнительны).

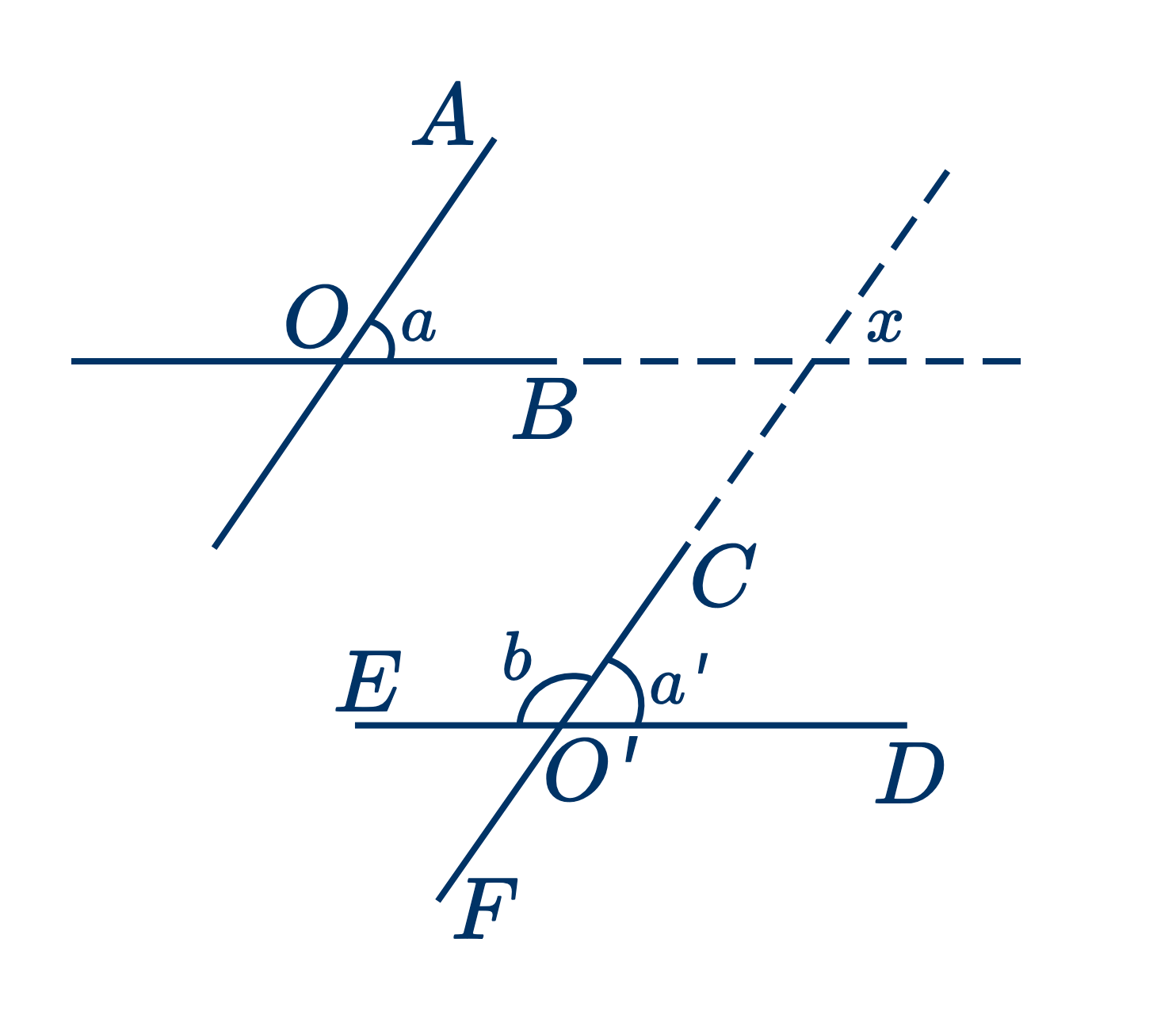
Дано: углы при вершинах $O$ и $O'$ со сторонами $OA$ и $OB$, соответственно параллельными $CF$ и $ED$.
Доказать, что угол $a=a'$ и $a+b=2$ прямым углам.

Продолжим $OB$ и $O'C$, пока они не пересекутся.
Тогда $a=x$ и $a'=x$ как соответственные углы при параллельных прямых.
Поэтому $a=a'$ (см. акс. 1.)
Кроме того $a'+b=2$ прямым углам. (см. теорему .)
Заменяем $a'$ равным ему углом $a$.
Получаем $a+b=2$ прямым углам.
Q.E.D.

Замечание.: Чтобы определить, когда углы равны и когда они пополнительны (рассматривают две прямые), мы замечаем у каждого угла правую и левую стороны, считая от вершины. (Так, $OA$ есть левая сторона $a$.) Если у двух углов правые стороны параллельны друг другу, так же как и левые, то такие углы равны. Если правая сторона одного угла параллельна левой стороне другого, и обратно, то такие углы пополнительны.

Таким образом, углы $a$ и $EO'F$, стороны которых параллельны: правая правой ($OB$ и $O'E$) и левая левой ($OA$ и $O'F$), равны; напротив, углы $a$ и $EO'C$, стороны которых параллельны: правая левой ($OB$ и $O'E$) и левая правой ($OA$ и $O'C$), пополнительны. Вы легко можете проверить это во всех 16 случаях, сравнивая каждый из 4 углов у вершины $O$ с каждым из четырех углов у вершины $O'$.

Теорема.

Два угла со взаимно-перпендикулярными сторонами или равны, или пополнительны.

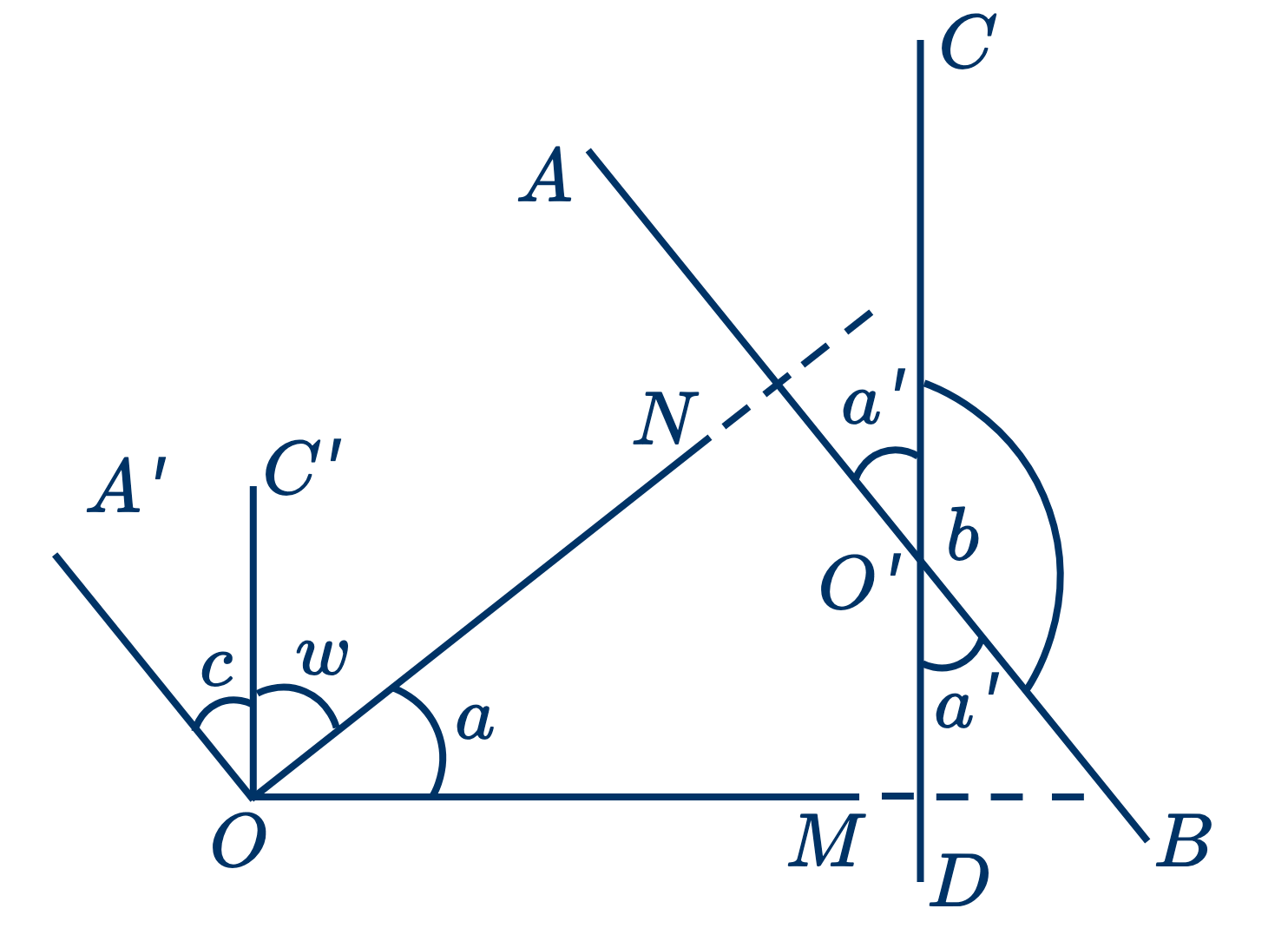
Дано: угол $NOM$ или $a$ и прямая $AB$ и $CD$, пересекающиеся в $O'$ и соответственно перпендикулярные к $ON$ и $OM$.
Доказать, что угол $a=a'$ и $a+b=2$ прямым углам.

Из точки $O$ проводим $OA'$, параллельную $AB$, и $OC$, параллельную $CD$.
$OA'$, будучи параллельна $AB$, перпендикулярна к $ON$. (см. теорему .)
По той же причине $OC'$, будучи параллельна $CD$, перпендикулярна к $OM$.
От каждого из прямых углов $A'ON$ и $C'OM$ отнимем общий угол $w$.
Тогда останется $c=a$. (см. акс. 3.)
Но $c=a'$ (см. теорему .)
Поэтому $a=a'$. (см. акс. 1.)
Кроме того $a'+b=2$ прямым углам. (Как смежные.) (см. теорему .)
Заменяя $a'$ равным углом $a$, получаем
$a+b=2$ прямым углам.
Q.E.D.

Замечание.: Углы равны, если их стороны взаимно-перпендикулярны: правая — правой, левая — левой сторонам; они пополнительны, если их стороны взаимно-перпендикулярны в противоположном (правая — левой) порядке.

Так, $a$ и $DO'B$, у которых правые стороны ($OM$ и $O'D$) взаимно-перпендикулярны и левые ($ON$ и $O'B$) также, равны и т.д.

← Читать дальше